Analyzing QMCPACK data
Using the qmc-fit tool for statistical time step extrapolation, trial wavefunction optimization and curve fitting
The qmc-fit tool is used to provide statistical estimates of curve-fitting parameters based on QMCPACK data.
qmc-fit is currently estimates fitting parameters related to time step extrapolation and trial wavefunction
optimization (optimal U for DFT+U, EXX fractions) and supports many types of fitted curves (e.g., Morse
potential binding curves and various equation-of-state fitting curves). An overview of all supported input flags to
qmc-fit can be obtained by typing qmc-fit -h at the command line:
>qmc-fit -h
usage: qmc-fit [-h] [-f FIT_FUNCTION] (-t TIMESTEPS | -u HUBBARDS | --exx EXX | --eos EOS) [-s SERIES_START] [-e EQUILS] [-b REBLOCK_FACTORS] [--noplot] {ts,u,eos} scalar_files [scalar_files ...]
This utility provides a fit to the one-dimensional parameter scans of QMC observables. Currently, the functionality in place is to fit linear/quadratic polynomial fits to the timestep VMC/DMC studies and single parameter optimization of trial wavefunctions using DMC local
energies and quadratic, cubic and quartic fits and equation-of-state and Morse potential fits.
positional arguments:
{ts,u,eos} One dimensional parameter used to fit QMC local energies. Options are ts for timestep and u for hubbard_u parameter fitting
scalar_files Scalar files used in the fit. An explicit list of scalar files with space or a wildcard (e.g. dmc*/dmc.s001.scalar.dat) is acceptable.
optional arguments:
-h, --help show this help message and exit
-f FIT_FUNCTION, --fit FIT_FUNCTION
Fitting function, options are (for each fit type) ts:{linear, quadratic, sqrt} u:{cubic, quadratic, quartic} eos:{birch, morse, murnaghan, vinet}. (default: linear)
-t TIMESTEPS Timesteps corresponding to scalar files, excluding any prior to --series_start (default: None)
-u HUBBARDS Hubbard U values (eV) (default: None)
--exx EXX EXX ratios (default: None)
--eos EOS Structural parameter for EOS fitting (volume or distance) (default: None)
-s SERIES_START, --series_start SERIES_START
Series number for first DMC run. Use to exclude prior VMC scalar files if they have been provided (default: None)
-e EQUILS, --equils EQUILS
Equilibration lengths corresponding to scalar files, excluding any prior to --series_start. Can be a single value for all files. If not provided, equilibration periods will be estimated. (default: None)
-b REBLOCK_FACTORS, --reblock_factors REBLOCK_FACTORS
Reblocking factors corresponding to scalar files, excluding any prior to --series_start. Can be a single value for all files. If not provided, reblocking factors will be estimated. (default: None)
--noplot Do not show plots. (default: False)
The jackknife statistical technique
The qmc-fit tool obtains estimates of fitting parameter means and
associated error bars via the “jack-knife” technique. This technique is
a powerful and general tool to obtain meaningful error bars for any
quantity that is related in a nonlinear fashion to an underlying set of
statistical data. For this reason, we give a brief overview of the
jackknife technique before proceeding with usage instructions for the
qmc-fit tool.
Consider \(N\) statistical variables \(\{x_n\}_{n=1}^N\) that have been outputted by one or more simulation runs. If we have \(M\) samples of each of the \(N\) variables, then the mean values of each these variables can be estimated in the standard way, that is, \(\bar{x}_n\approx \tfrac{1}{M}\sum_{m=1}^Mx_{nm}\).
Suppose we are interested in \(P\) statistical quantities \(\{y_p\}_{p=1}^P\) that are related to the original \(N\) variables by a known multidimensional function \(F\):
The relationship implied by \(F\) is completely general. For example, the \(\{x_n\}\) might be elements of a matrix with \(\{y_p\}\) being the eigenvalues, or \(F\) might be a fitting procedure for \(N\) energies at different time steps with \(P\) fitting parameters. An approximate guess at the mean value of \(\vec{y}\) can be obtained by evaluating \(F\) at the mean value of \(\vec{x}\) (i.e. \(F(\bar{x}_1\ldots\bar{x}_N)\)), but with this approach we have no way to estimate the statistical error bar of any \(\bar{y}_p\).
In the jackknife procedure, the statistical variability intrinsic to the underlying data \(\{x_n\}\) is used to obtain estimates of the mean and error bar of \(\{y_p\}\). We first construct a new set of \(x\) statistical data by taking the average over all samples but one:
The result is a distribution of approximate \(x\) mean values. These are used to construct a distribution of approximate means for \(y\):
Estimates for the mean and error bar of the quantities of interest can finally be obtained using the following formulas:
Performing time step extrapolation
In this section, we use a 32-atom supercell of MnO as an example system
for time step extrapolation. Data for this system has been collected in
DMC using the following sequence of time steps:
\(0.04,~0.02,~0.01,~0.005,~0.0025,~0.00125\) Ha\(^{-1}\). For
a typical production pseudopotential study, time steps in the range of
\(0.02-0.002\) Ha\(^{-1}\) are usually sufficient and it is
recommended to increase the number of steps/blocks by a factor of two
when the time step is halved. To perform accurate statistical fitting,
we must first understand the equilibration and autocorrelation
properties of the inputted local energy data. After plotting the local
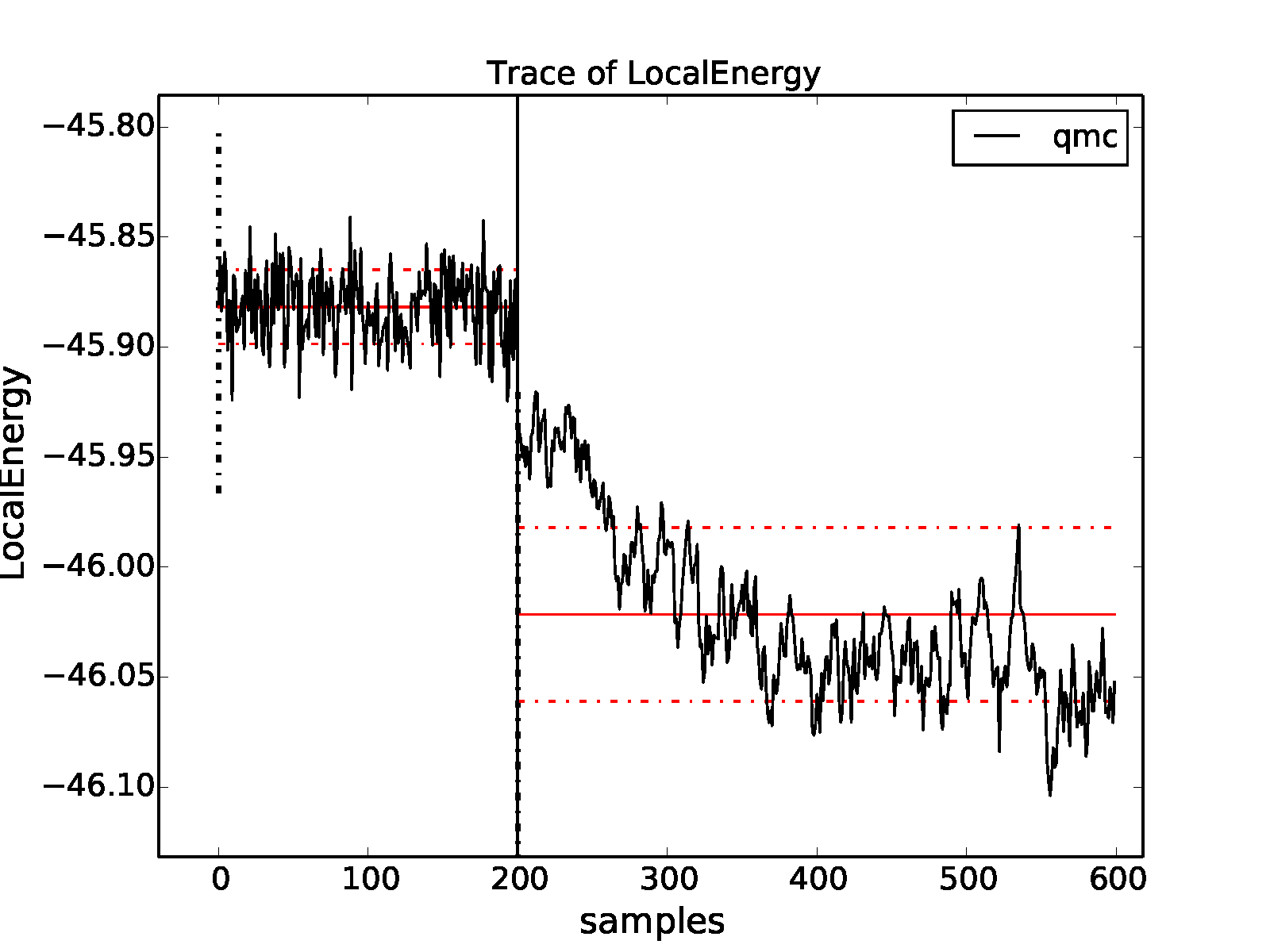
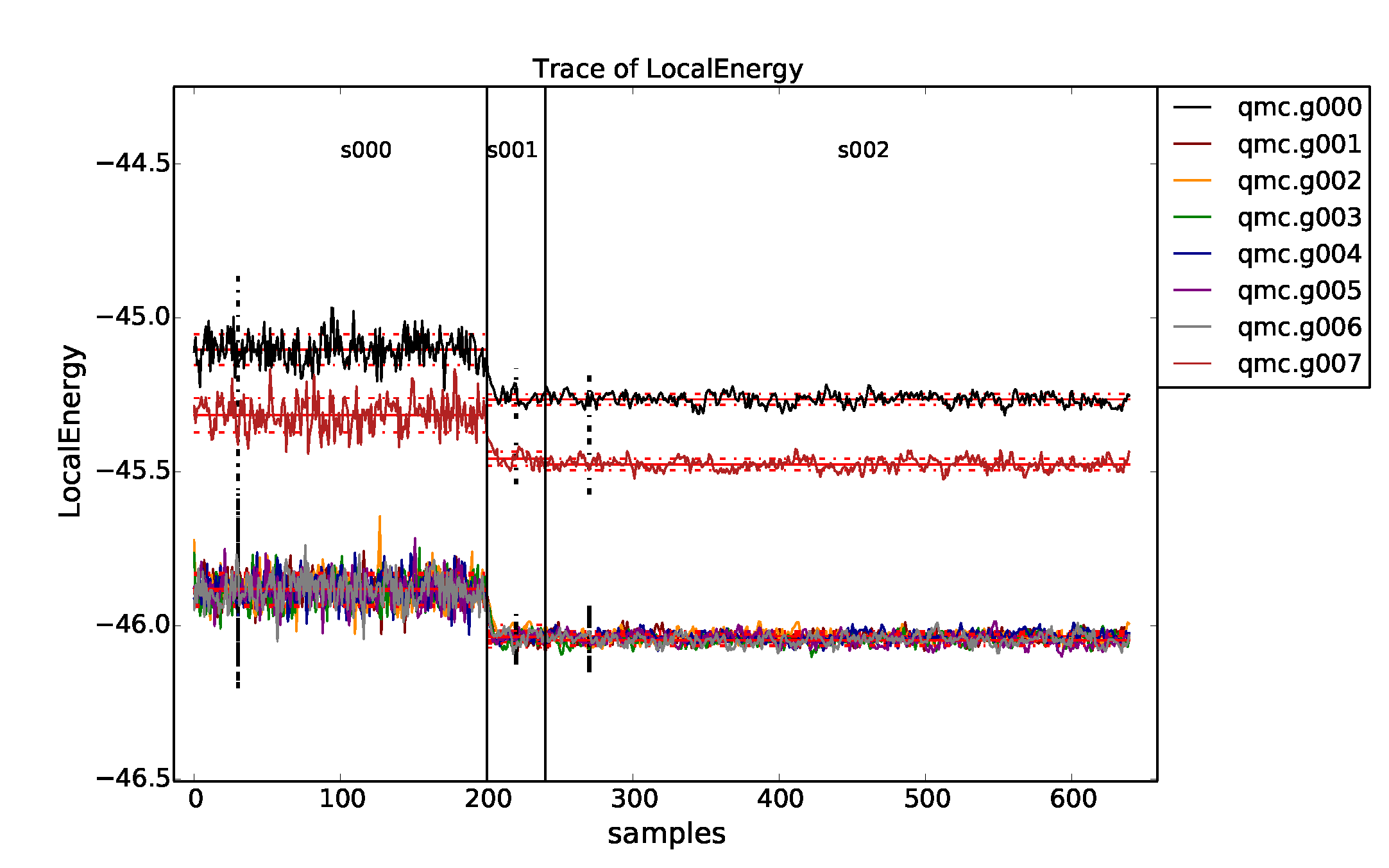
energy traces (qmca -t -q e -e 0 ./qmc*/*scalar*), it is clear that
an equilibration period of \(30\) blocks is reasonable. Approximate
autocorrelation lengths are also obtained with qmca:
>qmca -e 30 -q e --sac ./qmc*/qmc.g000.s002.scalar.dat
./qmc_tm_0.00125/qmc.g000 series 2 LocalEnergy = -3848.234513 +/- 0.055754 1.7
./qmc_tm_0.00250/qmc.g000 series 2 LocalEnergy = -3848.237614 +/- 0.055432 2.2
./qmc_tm_0.00500/qmc.g000 series 2 LocalEnergy = -3848.349741 +/- 0.069729 2.8
./qmc_tm_0.01000/qmc.g000 series 2 LocalEnergy = -3848.274596 +/- 0.126407 3.9
./qmc_tm_0.02000/qmc.g000 series 2 LocalEnergy = -3848.539017 +/- 0.075740 2.4
./qmc_tm_0.04000/qmc.g000 series 2 LocalEnergy = -3848.976424 +/- 0.075305 1.8
The autocorrelation must be removed from the data before jackknifing, so we will reblock the data by a factor of 4.
The qmc-fit tool can be used in the following way to obtain a linear
time step fit of the data:
>qmc-fit ts -e 30 -b 4 -s 2 -t '0.00125 0.0025 0.005 0.01 0.02 0.04' ./qmc*/*scalar*
fit function : linear
fitted formula: (-3848.193 +/- 0.037) + (-18.95 +/- 1.95)*t
intercept : -3848.193 +/- 0.037 Ha
The input arguments are as follows: ts indicates we are performing a
time step fit, -e 30 is the equilibration period removed from each
set of scalar data, -b 4 indicates the data will be reblocked by a
factor of 4 (e.g., a file containing 400 entries will be block averaged
into a new set of 100 before jackknife fitting), -s 2 indicates that
the time step data begins with series 2 (scalar files matching
*s000* or *s001* are to be excluded), and -t ‘0.00125 0.0025
0.005 0.01 0.02 0.04’ provides a list of time step values corresponding
to the inputted scalar files. The -e and -b options can receive
a list of file-specific values (same format as -t) if desired. As
can be seen from the text output, the parameters for the linear fit are
printed with error bars obtained with jackknife resampling and the zero
time step “intercept” is \(-3848.19(4)\) Ha. In addition to text
output, the previous command will result in a plot of the fit with the
zero time step value shown as a red dot, as shown in the top panel of
Fig. 12.
Different fitting functions are supported via the -f option.
Currently supported options include linear (\(a+bt\)),
quadratic (\(a+bt+ct^2\)), and sqrt
(\(a+b\sqrt{t}+ct\)). Results for a quadratic fit are shown
subsequently and in the bottom panel of Fig. 12.
>qmc-fit ts -f quadratic -e30 -b4 -s2 -t '0.00125 0.0025 0.005 0.01 0.02 0.04' ./qmc*/*scalar*
fit function : quadratic
fitted formula: (-3848.245 +/- 0.047) + (-7.25 +/- 8.33)*t + (-285.00 +/- 202.39)*t^2
intercept : -3848.245 +/- 0.047 Ha
In this case, we find a zero time step estimate of \(-3848.25(5)\) Ha\(^{-1}\). A time step of \(0.04\) Ha\(^{-1}\) might be on the large side to include in time step extrapolation, and it is likely to have an outsize influence in the case of linear extrapolation. Upon excluding this point, linear extrapolation yields a zero timestep value of \(-3848.22(4)\) Ha\(^{-1}\). Note that quadratic extrapolation can result in intrinsically larger uncertainty in the extrapolated value. For example, when the \(0.04\) Ha\(^{-1}\) point is excluded, the uncertainty grows by 50% and we obtain an estimated value of \(-3848.28(7)\) instead.
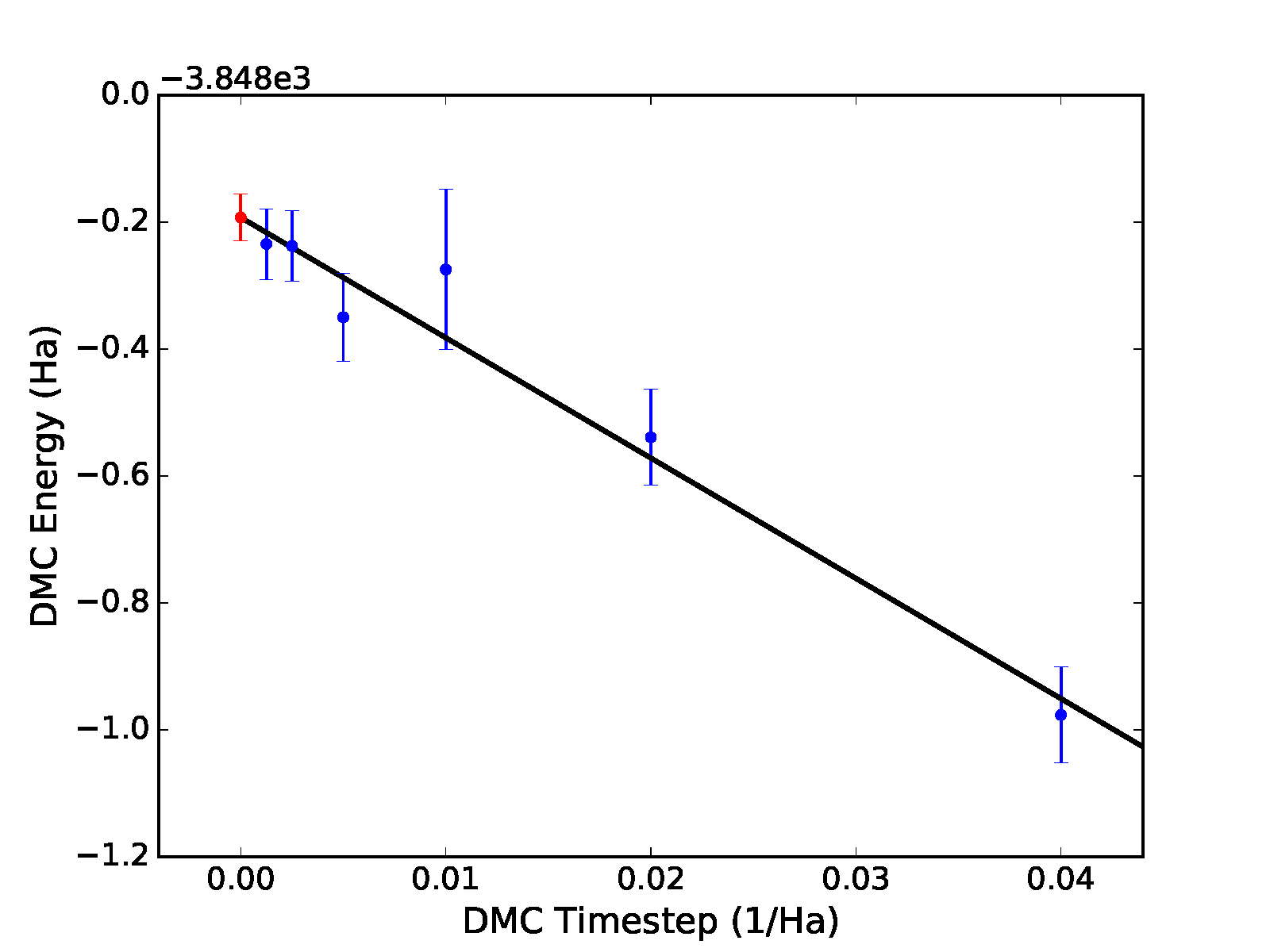
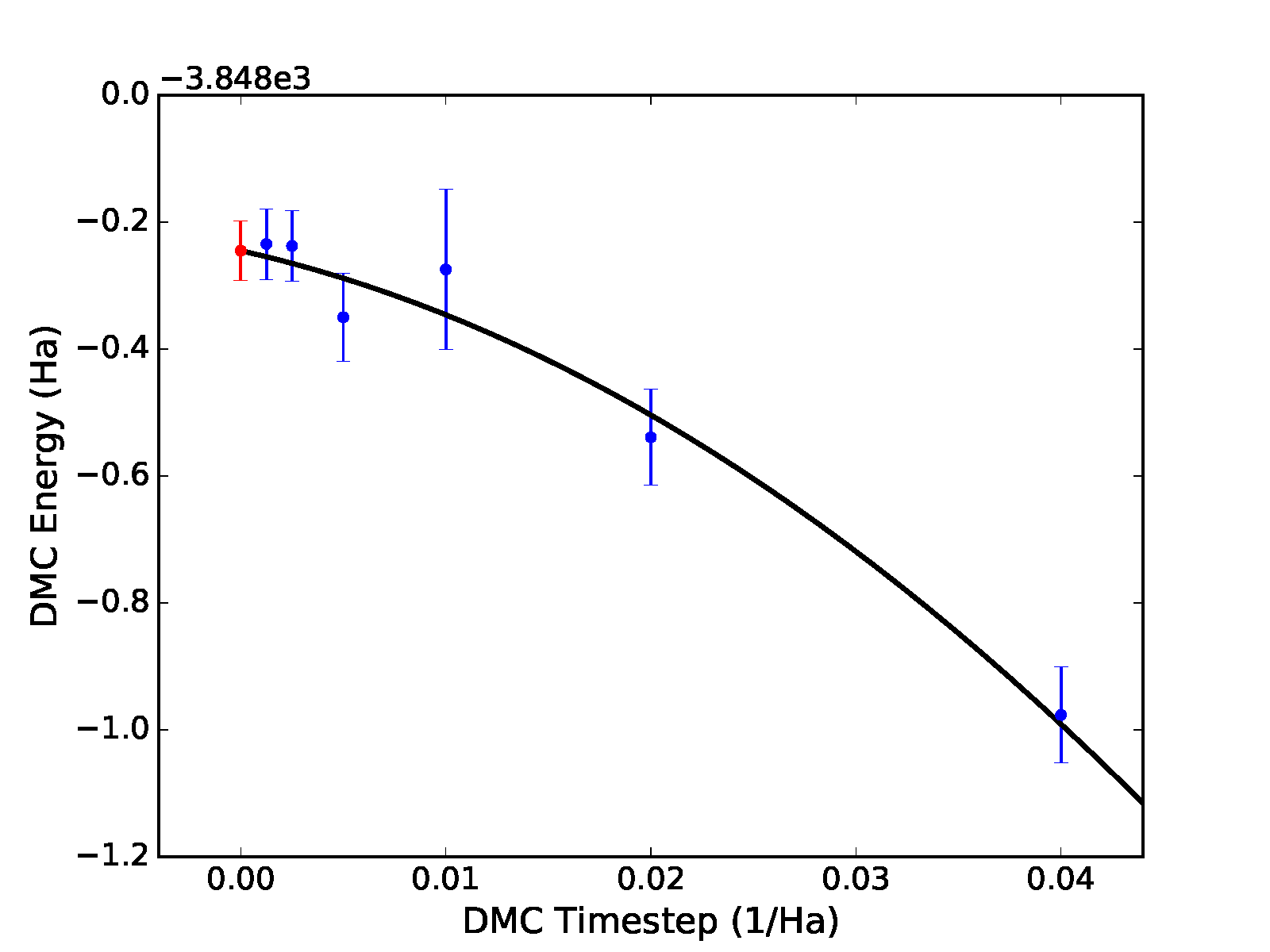
Fig. 12 Linear (top) and quadratic (bottom) time step fits to DMC data for a 32-atom supercell of MnO obtained with qmc-fit. Zero time step estimates are indicated by the red data point on the left side of either panel.
Performing trial wavefunction optimization fitting, e.g., to find optimal DFT+U
In this section, we use a 24-atom supercell of monolayer FeCl2 as an example system for wavefunction optimization
fitting. Using single determinant DFT wavefunctions, a practical method to perform wavefunction optimization is done through
scanning the Hubbard-U parameter in a DFT+U calculation used to generate the trial wavefunction. Similarly, one can also scan
different exact exchange ratio parameters in hybrid-DFT calculations. Here, we will show an example of this fitting for the
Hubbard-U parameter, but the same procedure can be applied to any single-parameter scans of trial wavefunctions. Data for this
system has been collected in DMC using the following sequence of Hubbard-U values on Fe-d orbitals: \(0 1 2 3 4 5\) eV. Some
non-zero U value often minimizes the DMC energy, but optimized U values have limited transferability across different systems.
Similar to the procedure for performing timestep statistical fitting, the quality of the input statistics must be checked using
qmca utility to determine the reblocking factor and equilibration periods. Assuming that an equilibration period of initial 50
steps, -e 50, and a reblocking period of 4, -b 6, is sufficient to remove correlations in the statistical local energies,
the qmc-fit tool can be used in the following way to obtain a quadratic fit of the data:
>qmc-fit u -e 50 -b 6 -u "0 1 2 3 4 5" -f quadratic dmc_u_*/dmc.s001.scalar.dat
fit function : quadratic
fitted formula: (-1230.1071 +/- 0.0045) + (-0.0683 +/- 0.0040)*t + (0.00883 +/- 0.00077)*t^2
root 1 minimum_u : 3.87 +/- 0.14 eV
root 1 minimum_e : -1230.2391 +/- 0.0026 Ha
root 1 curvature : 0.0177 +/- 0.0015
Here, qmc-fit u indicates we are performing a Hubbard-U/exact-exchange ratio fit,
-u option provides a list of Hubbard-U values \(0 1 2 3 4 5\) corresponding to the auto-sorted
dmc scalar files with wildcard dmc_u_*/dmc.s001.scalar.dat. Here, qmc-fit command is invoked at a
directory where folders such as dmc_u_0_2x2x1, dmc_u_1_2x2x1, dmc_u_2_2x2x1 reside.
Here, the text output provides the U value (minimum_u) and local energies (minimum_e)
at the minima of the polynomial which falls within the range of Hubbard-U values provided in the command
line, e.g. from 0 to 5. Therefore, a U value of \(3.8(1)\) eV minimizes the DMC energy of the system.
The curvature is printed for informative purposes only, but a curvature with small error bar could
indicate a higher quality polynomial fit. Similar to the timestep fit, a plot of the fit will also
produced as default where the minima of the polynomial is shown as a red dot as in Fig. 15.
Different fitting functions are supported via the -f option.
Currently supported options include quadratic (\(a+bt+ct^2\)), and
cubic (\(a+bt+ct^2+dt^3\)) and quartic (\(a+bt+ct^2+dt^3+et^4\)).
An example of a cubic fit is given as below:
>qmc-fit u -e 50 -b 6 -u "0 1 2 3 4 5" -f cubic dmc_u_*/dmc.s001.scalar.dat
fit function : cubic
fitted formula: (-1230.1087 +/- 0.0045) + (-0.0608 +/- 0.0073)*t + (0.0047 +/- 0.0033)*t^2 + (0.00055 +/- 0.00041)*t^3
root 1 minimum_u : 3.85 +/- 0.11 eV
root 1 minimum_e : -1230.2415 +/- 0.0033 Ha
root 1 curvature : 0.0221 +/- 0.0034
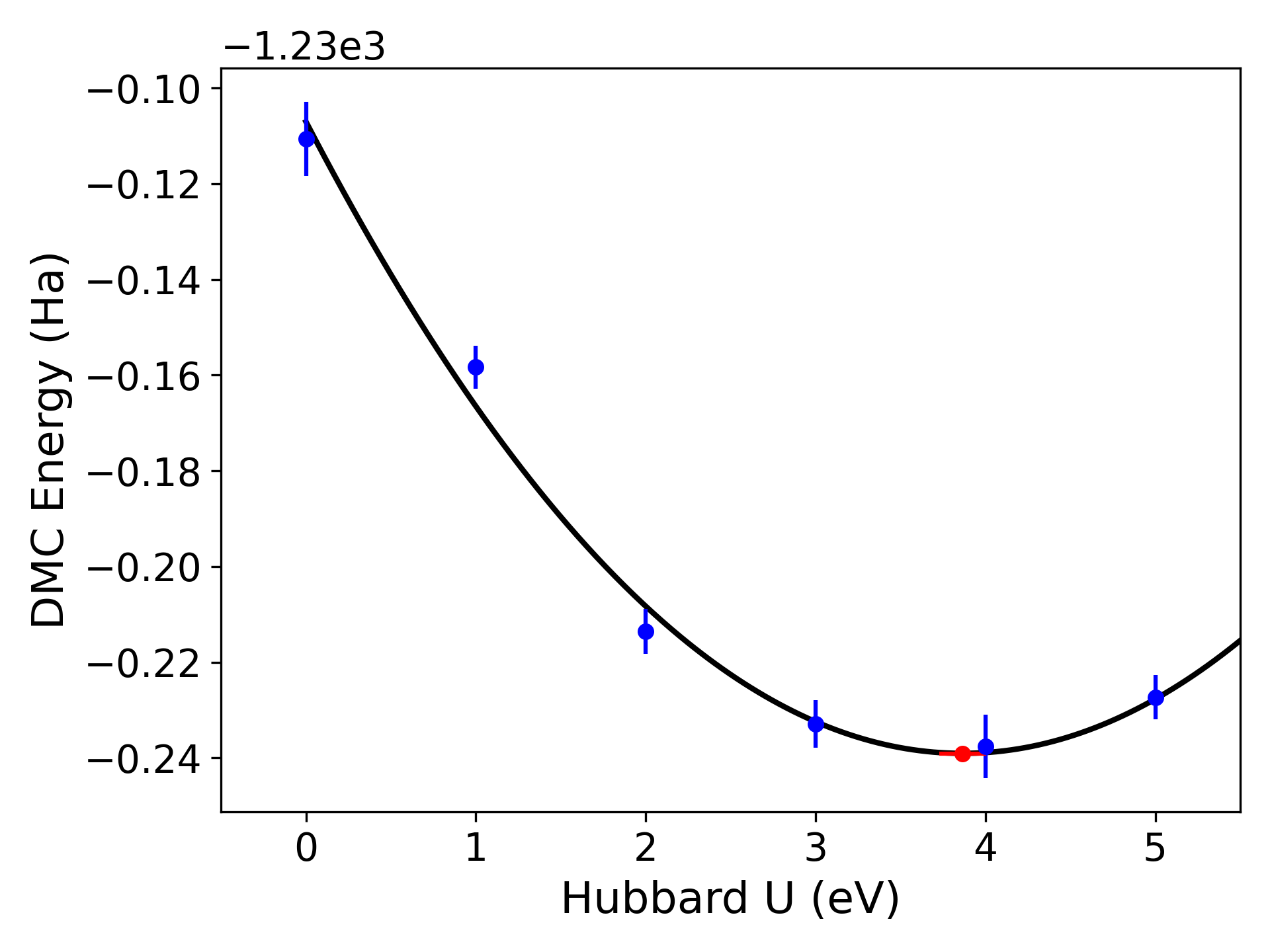
Fig. 13 Quadratic Hubbard-U fits to DMC data for a 24-atom supercell of monolayer FeCl2 obtained with qmc-fit. DMC local energy minima are indicated by the red data point on the bottom halves of either panel.
Performing equation-of-state and Morse potential binding curve fits
For a systematic series of statistical data, such as QMC calculations performed at different interatomic distances, or at a series of volumes
for an equation-of-states calculation, it is advised to perform jackknife fitting to determine quantities such as equilibrium distance, volume and
bulk moduli. For interatomic distances and equation of states fits to QMC calculations, qmc-fit has the capability to perform Morse and Birch, Murnaghan
and Vinet equation-of-state fits. In this example, we determine the equilibrium volume and bulk modulus of C-diamond using a 16 atom supercell using DMC and Murnaghan
equation-of-state fit. For the 16 atom supercell, we uniformly scan over the volumes between \(78.16\) and \(99.62 A^3\). Assuming that all these DMC calculation
folders are located under the same parent folder and ordered from smaller to the large volume (e.g. dmc_78.16, dmc_80.65 …), the following script can be used to make a
Murnaghan fit to the DMC energies.
>qmc-fit eos -e 50 -b 6 --eos "78.16 80.65 83.20 85.80 88.46 91.16 93.92 96.74 99.62" --fit murnaghan dmc_*/dmc.s001.scalar.dat
fit function : murnaghan
fitted formula: E_inf + B/Bp*V*((V_0/V)**Bp/(Bp-1)+1)-V_0*B/(Bp-1)
minimum_x: 89.00 +/- 0.12
e_inf: -91.2659 +/- 0.0012
B: 0.1053 +/- 0.0050
Bp: 0.000189 +/- 0.000011
pressure: -0.00000 +/- 0.00015
Here, the minimum volume is reported as \(89.00 \pm 0.12A^3\) consistent with the input volume units. Considering that this is a 16-atom cell, the per atom
quantity would be \(5.56 \pm 0.01 A^3\) per C. Bulk modulus, B, is reported as \(0.1053 \pm 0.005 Ha/A^3\). In SI units, this bulk modulus value corresponds to
\(459 \pm 21\) GPa. Different fitting functions are supported via the -f option. Currently supported options include Vinet , Murnaghan, Birch and Morse.
For more information and default options, please refer to qmc-fit -h.
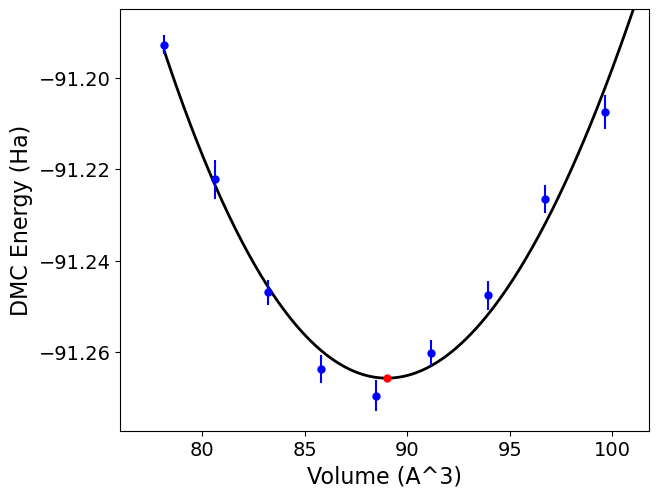
Fig. 14 Murnaghan equation-of-state fits to DMC data for a 16-atom supercell of C-diamond obtained with qmc-fit. DMC structural minimum is indicated by the red data point with an error bar smaller than its marker size.
Using the qdens tool to obtain electron densities
The qdens tool is provided to post-process the heavy density data
produced by QMCPACK and output the mean density (with and without
errorbars) in file formats viewable with, e.g., XCrysDen or VESTA. The
tool currently works only with the SpinDensity estimator in QMCPACK.
Note: this tool is provisional and may be changed or replaced at any
time. The planned successor to this tool (qstat) will expand access
to other observables and will retain at least the non-plotting
capabilities of qdens.
To use qdens, Nexus must be installed along with NumPy and H5Py. A
short list of example use cases are covered in the next section. Current
input flags are:
>qdens
Usage: qdens [options] [file(s)]
Options:
--version show program's version number and exit
-h, --help Print help information and exit (default=False).
-v, --verbose Print detailed information (default=False).
-f FORMATS, --formats=FORMATS
Format or list of formats for density file output.
Options: dat, xsf, chgcar (default=None).
-e EQUILIBRATION, --equilibration=EQUILIBRATION
Equilibration length in blocks (default=0).
-r REBLOCK, --reblock=REBLOCK
Block coarsening factor; use estimated autocorrelation
length (default=None).
-a, --average Average over files in each series (default=False).
-w WEIGHTS, --weights=WEIGHTS
List of weights for averaging (default=None).
-i INPUT, --input=INPUT
QMCPACK input file containing structure and grid
information (default=None).
-s STRUCTURE, --structure=STRUCTURE
File containing atomic structure (default=None).
-g GRID, --grid=GRID Density grid dimensions (default=None).
-c CELL, --cell=CELL Simulation cell axes (default=None).
--density_cell=DENSITY_CELL
Density cell axes (default=None).
--density_corner=DENSITY_CORNER
Density cell corner (default=None).
--lineplot=LINEPLOT Produce a line plot along the selected dimension: 0,
1, or 2 (default=None).
--noplot Do not show plots interactively (default=False).
--twist_info=TWIST_INFO
Use twist weights in twist_info.dat files or not.
Options: "use", "ignore", "require". "use" means use
when present, "ignore" means do not use, "require"
means must be used (default=use).
Usage examples
Process a single file, excluding the first 40 blocks, and produce XSF files:
qdens -v -e 40 -f xsf -i qmc.in.xml qmc.s000.stat.h5
Process files for all available series:
qdens -v -e 40 -f xsf -i qmc.in.xml *stat.h5
Combine groups of 10 adjacent statistical blocks together (appropriate if the estimated autocorrelation time is about 10 blocks):
qdens -v -e 40 -r 10 -f xsf -i qmc.in.xml qmc.s000.stat.h5
Apply different equilibration lengths and reblocking factors to each
series (below is appropriate if there are three series, e.g. s000,
s001, and s002):
qdens -v -e '20 20 40' -r '4 4 8' -f xsf -i qmc.in.xml *stat.h5
Produce twist averaged densities (also works with multiple series and reblocking):
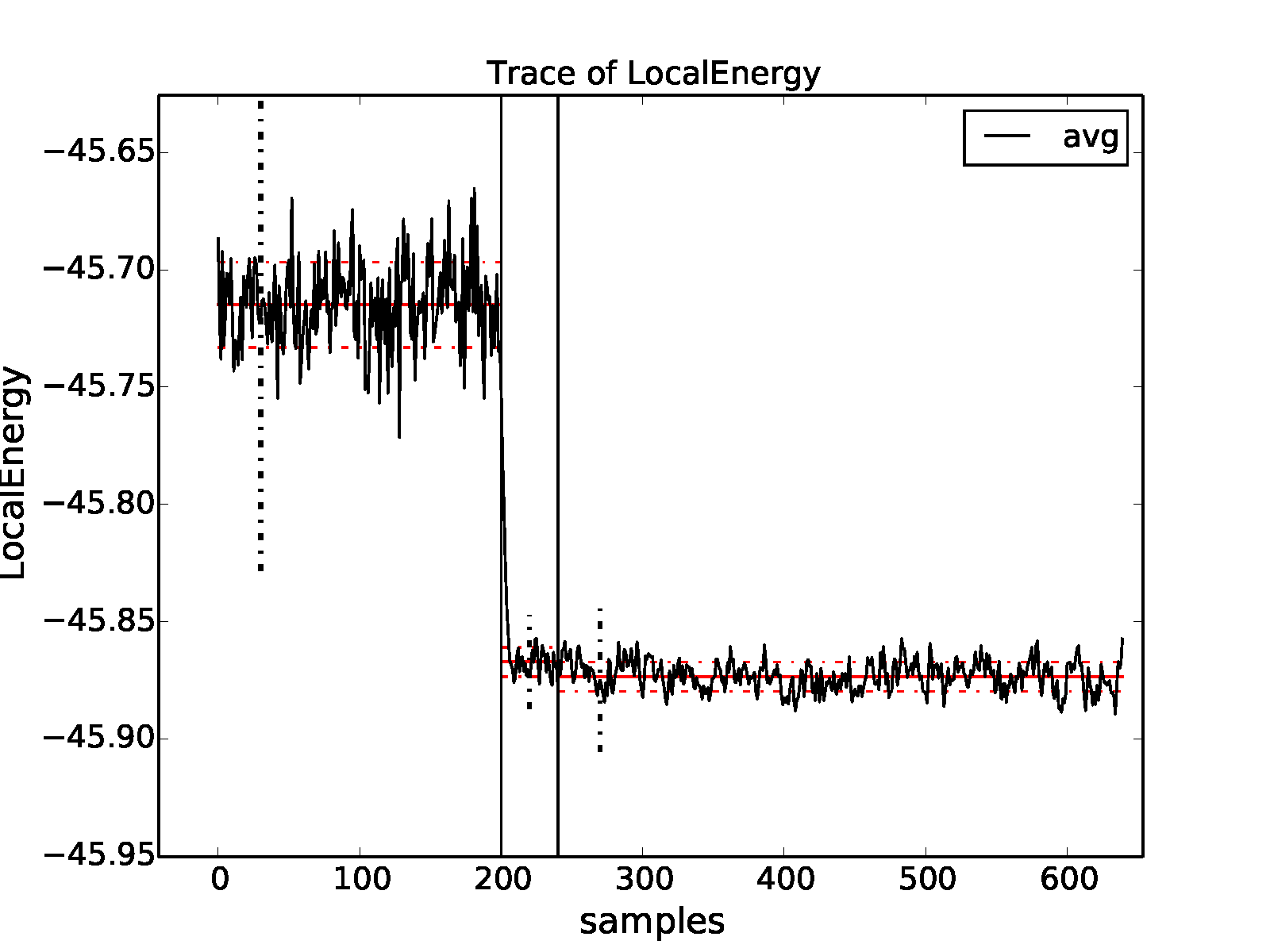
qdens -v -a -e 40 -f xsf -i qmc.g000.twistnum_0.in.xml qmc.g*.s000.stat.h5
Twist averaging with arbitrary weights can be performed via the -w
option in a fashion identical to qmca.
Files produced
Look for files with names and extensions similar to:
qmc.s000.SpinDensity_u.xsf
qmc.s000.SpinDensity_u-err.xsf
qmc.s000.SpinDensity_u+err.xsf
qmc.s000.SpinDensity_d.xsf
qmc.s000.SpinDensity_d-err.xsf
qmc.s000.SpinDensity_d+err.xsf
qmc.s000.SpinDensity_u+d.xsf
qmc.s000.SpinDensity_u+d-err.xsf
qmc.s000.SpinDensity_u+d+err.xsf
qmc.s000.SpinDensity_u-d.xsf
qmc.s000.SpinDensity_u-d-err.xsf
qmc.s000.SpinDensity_u-d+err.xsf
Files postfixed with u relate to the up electron density, d to
down, u+d to the total charge density, and u-d to the difference
between up and down electron densities.
Files without err in the name contain only the mean, whereas files
with +err/-err in the name contain the mean plus/minus the
estimated error bar. Please use caution in interpreting the error bars
as their accuracy depends crucially on a correct estimation of the
autocorrelation time by the user (see -r option) and having a
sufficient number of blocks remaining following any reblocking.
When twist averaging, the group tag (e.g. g000 or similar) will be
replaced with avg in the names of the outputted files.
Using the qdens-radial tool to estimate atomic occupations
Once the *Density*.xsf files are obtained from qdens, one can use the qdens-radial tool to calculate the on-site populations.
Given a set of species and radii (in Angstroms), this tool will generate a radial density – angular average – around the atomic sites up to the specified radius.
The radial density can be chosen to be non-cumulative or cumulative (integrated).
>qdens-radial
Usage: qdens-radial [options] xsf_file
Options:
--version show program's version number and exit
-h, --help Print help information and exit (default=False).
-v, --verbose Print detailed information (default=False).
-r RADII, --radii=RADII
List of cutoff radii (default=None).
-s SPECIES, --species=SPECIES
List of species (default=None).
-a APP, --app=APP Source that generated the .xsf file. Options: "pwscf",
"qmcpack" (default=qmcpack).
-c, --cumulative Evaluate cumulative radial density at cutoff radii
(default=False).
--vmc=VMC_FILE Location of VMC to be used for extrapolating mixed-
estimator bias (default=None).
--write Write extrapolated values to qmc-extrap.xsf
(default=False).
--vmcerr=VMC_ERR_FILE
Location of VMC+err to be used for extrapolating
mixed-estimator bias and resampling (default=None).
--dmcerr=DMC_ERR_FILE
Location of DMC+err to be used for resampling
(default=None).
--seed=RANDOM_SEED Random seed used for re-sampling. (default=None).
-n NSAMPLES, --nsamples=NSAMPLES
Number of samples for resampling (default=50).
-p, --plot Show plots interactively (default=False).
Usage examples
Below are example use cases for the H2O molecule using DMC data.
Plot DMC non-cumulative radial density of the O atom:
qdens-radial -p -s O -r 1 dmc.s002.Density_q.xsf
Plot DMC cumulative radial density of the O atom:
qdens-radial -p -s O -r 1 -c dmc.s002.Density_q.xsf
For the cumulative case, qdens-radial will also print the cumulative value at the specified radius, i.e., an estimate of the atomic occupation.
Estimate of the DMC atomic occupation:
qdens-radial -p -s O -r 1.1 -c dmc.s002.Density_q.xsf
Output:
Cumulative Value of O Species at Cutoff 1.1 is: 6.55517033828574
One can also get an extrapolated estimate (mixed-estimator bias) for this quantity by providing a VMC .xsf file.
Estimate of the extrapolated atomic occupation:
qdens-radial -p -s O -r 1.1 -c --vmc=dmc.s000.Density_q.xsf dmc.s002.Density_q.xsf
Output:
Extrapolating from VMC and DMC densities...
Cumulative Value of O Species at Cutoff 1.1 is: 6.576918233167152
Error bars
One can “resample” the density at each grid point to obtain an estimate of the error bar. Recipe:
1. Use error bars from *.Density_q+err.xsf file and draw samples from a Gaussian
distribution with a standard deviation that matches the error bar.
2. Calculate occupations with resampled data and calculate standard deviation
to obtain the error bar on the occupation.
3. Make sure the number of samples (-n) is converged.
Estimate DMC atomic occupation with error bar:
qdens-radial -p -s O -r 1.1 -c -n 20 --dmcerr=dmc.s002.Density_q+err.xsf dmc.s002.Density_q.xsf
Output:
Resampling to obtain error bar (NOTE: This can be slow)...
Will compute 20 samples...
...
Cumulative Value of O Species at Cutoff 1.1 is: 6.55517033828574+/-0.001558553749396279