Development Guide
The section gives guidance on how to extend the functionality of QMCPACK. Future examples will likely include topics such as the addition of a Jastrow function or a new QMC method.
Definitions
Legacy: code from previous work usually not in line current coding standards or design. It is mostly functional and correct within the context of legacy operations. Most has been modified piecemeal for years to extend functionality.
Refactoring: Process of redesigning code in place through incremental changes toward current design and functionality goals.
QMCPACK coding standards
This chapter presents what we collectively have agreed are best practices for the code. This includes formatting style, naming conventions, documentation conventions, and certain prescriptions for C++ language use. At the moment only the formatting can be enforced in an objective fashion.
New development should follow these guidelines, and contributors are expected to adhere to them as they represent an integral part of our effort to continue QMCPACK as a world-class, sustainable QMC code. Although some of the source code has a ways to go to live up to these ideas, new code, even in old files, should follow the new conventions not the local conventions of the file whenever possible. Work on the code with continuous improvement in mind rather than a commitment to stasis.
The current workflow conventions for the project are described in the wiki on the GitHub repository. It will save you and all the maintainers considerable time if you read these and ask questions up front.
A PR should follow these standards before inclusion in the mainline. You can be sure of properly following the formatting conventions if you use clang-format. The mechanics of clang-format setup and use can be found at https://github.com/QMCPACK/qmcpack/wiki/Source-formatting.
The clang-format file found at qmcpack/src/.clang-format should be run over all code touched in a PR before a pull request is
prepared. We also encourage developers to run clang-tidy with the qmcpack/src/.clang-tidy configuration over all new code.
As much as possible, try to break up refactoring, reformatting, feature, and bugs into separate, small PRs. Aim for something that would take a reviewer no more than an hour. In this way we can maintain a good collective development velocity.
Files
Each file should start with the header.
//////////////////////////////////////////////////////////////////////////////////////
// This file is distributed under the University of Illinois/NCSA Open Source License.
// See LICENSE file in top directory for details.
//
// Copyright (c) 2021 QMCPACK developers
//
// File developed by: Name, email, affiliation
//
// File created by: Name, email, affiliation
//////////////////////////////////////////////////////////////////////////////////////
If you make significant changes to an existing file, add yourself to the list of “developed by” authors.
File organization
Header files should be placed in the same directory as their implementations. Unit tests should be written for all new
functionality. These tests should be placed in a tests subdirectory below the implementations.
File names
Each class should be defined in a separate file with the same name as the class name. Use separate .cpp implementation files
whenever possible to aid in incremental compilation.
The filenames of tests are composed by the filename of the object tested and the prefix test_. The filenames of fake and
mock objects used in tests are composed by the prefixes fake_ and mock_, respectively, and the filename of the object
that is imitated.
Header files
All header files should be self-contained (i.e., not dependent on following any other header when it is included). Nor should they include files that are not necessary for their use (i.e., headers needed only by the implementation). Implementation files should not include files only for the benefit of files they include.
There are many header files that currently violate this. Each header must use #define guards to prevent multiple inclusion.
The symbol name of the #define guards should be NAMESPACE(s)_CLASSNAME_H.
Includes
Related header files should be included without any path. Header files from external projects and standard libraries should be
includes using the <iostream> convention, while headers that are part of the QMCPACK project should be included using the
"our_header.h" convention.
We are now using a new header file inclusion style following the modern CMake transition in QMCPACK, while the legacy code may still use the legacy style. Newly written code and refactored code should be transitioned to the new style.
New style for modern CMake
In QMCPACK, include paths are handled by modern CMake target dependency. Every top level folder is at least one target. For
example, src/Particle/CMakeLists.txt defines qmcparticle target. It propagates include path qmcpack/src/Particle to
compiling command lines in CMake via
TARGET_INCLUDE_DIRECTORIES(qmcparticle PUBLIC "${CMAKE_CURRENT_SOURCE_DIR}")
For this reason, the file qmcpack/src/Particle/Lattice/ParticleBConds3DSoa.h should be included as
#include "Lattice/ParticleBConds3DSoa.h"
If the compiled file is not part of the same target as qmcparticle, the target it belongs to should have a dependency on
qmcparticle. For example, test source files under qmcpack/src/Particle/tests are not part of qmcparticle and thus requires
the following additional CMake setting
TARGET_LINK_LIBRARIES(${UTEST_EXE} qmcparticle)
Legacy style
Header files should be included with the full path based on the src directory. For example, the file
qmcpack/src/QMCWaveFunctions/SPOSet.h should be included as
#include "QMCWaveFunctions/SPOSet.h"
Even if the included file is located in the same directory as the including file, this rule should be obeyed.
Ordering
For readability, we suggest using the following standard order of includes:
related header
std C library headers
std C++ library headers
Other libraries’ headers
QMCPACK headers
In each section the included files should be sorted in alphabetical order.
Naming
The balance between description and ease of implementation should be balanced such that the code remains self-documenting within a single terminal window. If an extremely short variable name is used, its scope must be shorter than \(\sim 40\) lines. An exception is made for template parameters, which must be in all CAPS. Legacy code contains a great variety of hard to read code style, read this section and do not imitate existing code that violates it.
Namespace names
Namespace names should be one word, lowercase.
Type and class names
Type and class names should start with a capital letter and have a capital letter for each new word. Underscores (_) are not
allowed. It’s redundant to end these names with Type or _t.
.. code:: c++
\no using ValueMatrix_t = Matrix<Value>; using RealType = double;
Variable names
Variable names should not begin with a capital letter, which is reserved for type and class names. Underscores (_) should be
used to separate words.
Class data members
Class private/protected data members names should follow the convention of variable names with a trailing underscore (_). The use of public member functions is discourage, rethink the need for it in the first place. Instead get and set functions are the preferred access method.
(Member) function names
Function names should start with a lowercase character and have a capital letter for each new word. The exception are the special cases for prefixed multiwalker (mw_) and flex (flex_) batched API functions. Coding convention should follow after those prefixes.
Template Parameters
Template parameters names should be in all caps with (_) separating words. It’s redundant to end these names with _TYPE,
Lambda expressions
Named lambda expressions follow the naming convention for functions:
auto myWhatever = [](int i) { return i + 4; };
Macro names
Macro names should be all uppercase and can include underscores (_). The underscore is not allowed as first or last character.
Test case and test names
Test code files should be named as follows:
class DiracMatrix;
//leads to
test_dirac_matrix.cpp
//which contains test cases named
TEST_CASE("DiracMatrix_update_row","[wavefunction][fermion]")
where the test case covers the updateRow and [wavefunction][fermion] indicates the test belongs to the fermion wavefunction functionality.
Formatting and “style”
Use the provided clang-format style in src/.clang-format to format .h, .hpp, .cu, and .cpp files. Many of the following rules will be applied to the code by clang-format, which should allow you to ignore most of them if you always run it on your modified code.
You should use clang-format support and the .clangformat file with your editor, use a Git precommit hook to run clang-format
or run clang-format manually on every file you modify. However, if you see numerous formatting updates outside of the code you
have modified, first commit the formatting changes in a separate PR.
Indentation
Indentation consists of two spaces. Do not use tabs in the code.
Line length
The length of each line of your code should be at most 120 characters.
Horizontal spacing
No trailing white spaces should be added to any line. Use no space before a comma (,) and a semicolon (;), and add a space
after them if they are not at the end of a line.
Preprocessor directives
The preprocessor directives are not indented. The hash is the first character of the line.
Binary operators
The assignment operators should always have spaces around them.
Unary operators
Do not put any space between an unary operator and its argument.
Types
The using syntax is preferred to typedef for type aliases. If the actual type is not excessively long or complex, simply
use it; renaming simple types makes code less understandable.
Pointers and references
Pointer or reference operators should go with the type. But understand the compiler reads them from right to left.
Type* var;
Type& var;
//Understand this is incompatible with multiple declarations
Type* var1, var2; // var1 is a pointer to Type but var2 is a Type.
Templates
The angle brackets of templates should not have any external or internal padding.
template<class C>
class Class1;
Class1<Class2<type1>> object;
Vertical spacing
Use empty lines when it helps to improve the readability of the code, but do not use too many. Do not use empty lines after a brace that opens a scope or before a brace that closes a scope. Each file should contain an empty line at the end of the file. Some editors add an empty line automatically, some do not.
Variable declarations and definitions
Avoid declaring multiple variables in the same declaration, especially if they are not fundamental types:
int x, y; // Not recommended Matrix a("my-matrix"), b(size); // Not allowed // Preferred int x; int y; Matrix a("my-matrix"); Matrix b(10);
Use the following order for keywords and modifiers in variable declarations:
// General type [static] [const/constexpr] Type variable_name; // Pointer [static] [const] Type* [const] variable_name; // Integer // the int is not optional not all platforms support long, etc. [static] [const/constexpr] [signedness] [size] int variable_name; // Examples: static const Matrix a(10); const double* const d(3.14); constexpr unsigned long l(42);
Function declarations and definitions
The return type should be on the same line as the function name. Parameters should also be on the same line unless they do not fit on it, in which case one parameter per line aligned with the first parameter should be used.
Also include the parameter names in the declaration of a function, that is,
// calculates a*b+c
double function(double a, double b, double c);
// avoid
double function(double, double, double);
// dont do this
double function(BigTemplatedSomething<double> a, BigTemplatedSomething<double> b,
BigTemplatedSomething<double> c);
// do this
double function(BigTemplatedSomething<double> a,
BigTemplatedSomething<double> b,
BigTemplatedSomething<double> c);
Conditionals
Examples:
if (condition)
statement;
else
statement;
if (condition)
{
statement;
}
else if (condition2)
{
statement;
}
else
{
statement;
}
Switch statement
Switch statements should always have a default case.
Example:
switch (var)
{
case 0:
statement1;
statement2;
break;
case 1:
statement1;
statement2;
break;
default:
statement1;
statement2;
}
Loops
Examples:
for (statement; condition; statement)
statement;
for (statement; condition; statement)
{
statement1;
statement2;
}
while (condition)
statement;
while (condition)
{
statement1;
statement2;
}
do
{
statement;
}
while (condition);
Class format
public, protected, and private keywords are not indented.
Example:
class Foo : public Bar
{
public:
Foo();
explicit Foo(int var);
void function();
void emptyFunction() {}
void setVar(const int var)
{
var_ = var;
}
int getVar() const
{
return var_;
}
private:
bool privateFunction();
int var_;
int var2_;
};
Constructor initializer lists
Examples:
// When everything fits on one line:
Foo::Foo(int var) : var_(var)
{
statement;
}
// If the signature and the initializer list do not
// fit on one line, the colon is indented by 4 spaces:
Foo::Foo(int var)
: var_(var), var2_(var + 1)
{
statement;
}
// If the initializer list occupies more lines,
// they are aligned in the following way:
Foo::Foo(int var)
: some_var_(var),
some_other_var_(var + 1)
{
statement;
}
// No statements:
Foo::Foo(int var)
: some_var_(var) {}
Namespace formatting
The content of namespaces is not indented. A comment should indicate when a namespace is closed. (clang-format will add these if absent). If nested namespaces are used, a comment with the full namespace is required after opening a set of namespaces or an inner namespace.
Examples:
namespace ns
{
void foo();
} // ns
namespace ns1
{
namespace ns2
{
// ns1::ns2::
void foo();
namespace ns3
{
// ns1::ns2::ns3::
void bar();
} // ns3
} // ns2
namespace ns4
{
namespace ns5
{
// ns1::ns4::ns5::
void foo();
} // ns5
} // ns4
} // ns1
QMCPACK C++ guidance
The guidance here, like any advice on how to program, should not be treated as a set of rules but rather the hard-won wisdom of many hours of suffering development. In the past, many rules were ignored, and the absolute worst results of that will affect whatever code you need to work with. Your PR should go much smoother if you do not ignore them.
Encapsulation
A class is not just a naming scheme for a set of variables and functions. It should provide a logical set of methods, could contain the state of a logical object, and might allow access to object data through a well-defined interface related variables, while preserving maximally ability to change internal implementation of the class.
Do not…
use
structas a way to avoid controlling access to the class. Only when the instantiated objects are public data structure isstructappropriate.use inheritance primarily as a means to break encapsulation. If your class could aggregate or compose another class, do that, and access it solely through its public interface. This will reduce dependencies.
pass entire classes as function arguments when what the function actually requires is one or a few arguments available through the public API of a class, encapsulation is harmful when is just used to save keystrokes and hides the logical data dependence of functions.
All these “idioms” are common in legacy QMCPACK code and should not be perpetuated.
Casting
In C++ source, avoid C style casts; they are difficult to search for and imprecise in function. Explicit C++ style casts make it clear what the safety of the cast is and what sort of conversion is expected to be possible.
Pre-increment and pre-decrement
Use the pre-increment (pre-decrement) operator when a variable is incremented (decremented) and the value of the expression is not used. In particular, use the pre-increment (pre-decrement) operator for loop counters where i is not used:
for (int i = 0; i < N; ++i)
{
doSomething();
}
for (int i = 0; i < N; i++)
{
doSomething(i);
}
The post-increment and post-decrement operators create an unnecessary copy that the compiler cannot optimize away in the case of iterators or other classes with overloaded increment and decrement operators.
Alternative operator representations
Alternative representations of operators and other tokens such as and, or, and not instead of &&, ||, and ! are not allowed.
For the reason of consistency, the far more common primary tokens should always be used.
Use of const
Add the
constqualifier to all function parameters that are not modified in the function body.For parameters passed by value, add only the keyword in the function definition.
Member functions should be specified const whenever possible.
// Declaration int computeFoo(int bar, const Matrix& m) // Definition int computeFoo(const int bar, const Matrix& m) { int foo = 42; // Compute foo without changing bar or m. // ... return foo; } class MyClass { int count_ ... int getCount() const { return count_;} }
Smart pointers
Use of smart pointers is being adopted to help make QMCPACK memory leak free. Prior to C++11, C++ uses C-style pointers. A C-style pointer can have several meanings and the ownership of a piece of help memory may not be clear. This leads to confusion and causes memory leaks if pointers are not managed properly. Since C++11, smart pointers were introduced to resolve this issue. In addition, it demands developers to think about the ownership and lifetime of declared pointer objects.
std::unique_ptr
A unique pointer is the unique owner of a piece of allocated memory. Pointers in per-walker data structure with distinct contents should be unique pointers. For example, every walker has a trial wavefunction object which contains an SPO object pointer. Because the SPO object has a vector to store SPO evaluation results, it cannot be shared between two trial wavefunction objects. For this reason the SPO object pointer should be an unique pointer.
In QMCPACK, most raw pointers can be directly replaced with std::unique_ptr.
Corresponding use of new operator can be replaced with std:make_unique.
Log and error output
app_log, app_warning, app_err and app_debug print out messages only on rank 0 to avoid repetitive messages from
every MPI rank. For this reason, they are only suitable for outputing messages identical to all MPI ranks. app_debug prints only
when --verbosity=debug command line option is used. Messages that come from only one or a few MPI ranks should use std::cout
and std::cerr.
If the code needs to be stopped after an unrecoverable error that happens uniformly on all the MPI ranks, a bad input for example,
avoid using app_err together with Communicate::abort(msg) or APP_ABORT(msg) because any MPI rank other than rank 0 may
stop the whole run before rank 0 is able to print out the error message. To secure the printout before stopping, use
Communicate::barrier_and_abort(msg) if an MPI communicator is available or throw a custom exception UniformCommunicateError
and capture it where Communicate::barrier_and_abort() can be used. Note that UniformCommunicateError can only be used for
uniform error, improper use may cause QMCPACK hanging.
In addition, avoid directly calling C function abort(), exit() and MPI_Abort() for stopping the code.
Modernized Input
Input Facts
The user supplied input to QMCPACK can be formally thought of as a tree constructed of input nodes. These nodes have optional attributes and content. Content may be nothing, free form “text” that must be handled in an application defined manner, or one or more nodes with the same possible structure. For most input classes the child nodes will consist primarily or entirely of
parameternodes.This tree is expressed by using XML as described previously in this manual. While XML offers the possibility that a formal specification could be defined, the documentation earlier in the manual is the most formal specification of the XML input format that exists.
Parameter nodes for historical reasons can be specified in two different ways.
<the_parameter_name>content</the_parameter_name>
<parameter name="the_parameter_name">content</parameter>
Legacy Input Problems
XML input parsing, validation, and processing takes place throughout the execution of the application, as needed through put, process and other calls to existing objects.
Most/All simulation objects are not valid at construction but are state machines (see Fig. 29) that require many transforms to become valid.
This impedes unit tests of simulation objects since the process for bring objects to a valid state must be derived via extensive code review or by mocking large portions of the applications execution sequence copied.
This impedes unit tests of input validation since to the degree this occurs is happens primarily as side effects to the construction of simulation objects.
Reasoning about the state of objects when debugging or developing new features is difficult.
Attributes are sometimes the main content or only content of a node.
Multiple objects will take the same node as an argument to their
putmethod, so ownership of nodes is unclear.In different input sections, different ways to specify very similar information. i.e. grids. are used.
Specific implementations of grids etc. are tangled up in the extended construction of numerous simulation objects and particular input expressions, this is a barrier to code reuse and improvement.
The XML parser catches only the most basic issues with the input document.
Unrecognized elements, parameter names, and attributes are silently ignored. Sometimes defaults are used instead.
Invalid input to recognized elements is sometimes checked, sometimes causes crashes, sometimes causes invalid answers (NaNs etc.) and sometimes is just fixed.
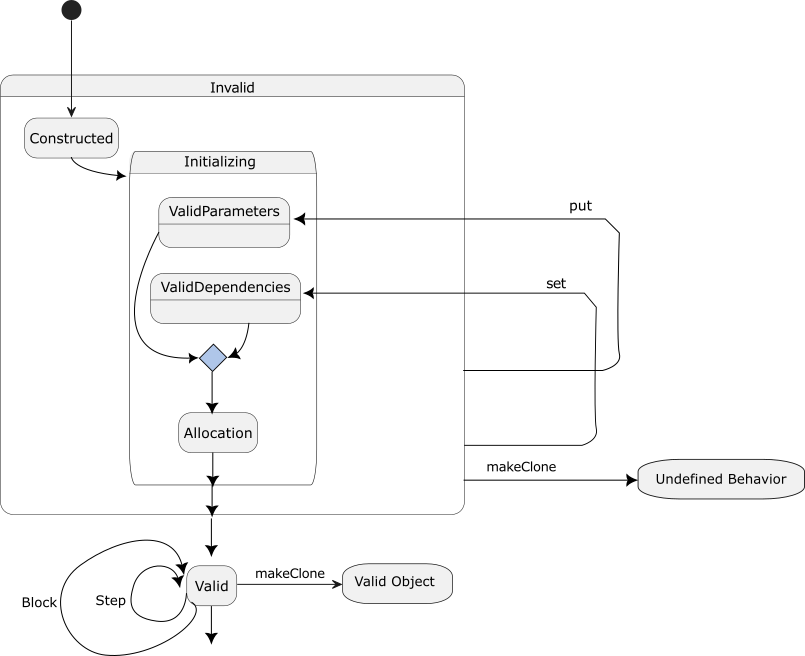
Fig. 29 Simulation object state diagram emphasizing the long period and multiple state updates required to become a valid object. Many objects require more than two updates to go from constructed to valid.
Modernizing Goals
Legacy QMCPACK input parsing is characterized by a unclear ownership of input nodes and a multistage mixture of construction, parsing, validation, and state progression of simulation objects. The handling of input and its relation to testing and error handling is a major pain point for developers. The following program is proposed:
Simulation classes and the input parsing and storage of input values should be refactored into 2 or more classes. Below these are refered to as Simulation classes and Input classes.
No input parsing should occur in simulation objects. i.e. no
putmethods, noXMLNodePtrargument types.Simulation objects should access input parameters as clearly defined and appropriate types through read only Input object accessors, they should not make local copies of these parameters.
Each type of Node in the input tree should have a clear relationship to some input class.
If an input class is given a node it must be able handle all content and attributes and able to handle or delegate all child nodes.
Anything other than white space in a node, attribute or element not consumed by the node owner or its delegates constitutes a fatal error.
The Input objects should be for practical purposes immutable after parsing.
After parsing the input parameters should be in appropriate native c++ types.
Default values should be specified in native c++ whenever practical.
In principle you should be able to construct an input object simply by initializing its members i.e. no input parsing necessary.
The Improved Input Design
Make input parsing and validation (to the degree feasible) distinct stages of application execution.
Improve separation of concerns
Facilitate unit testing
Allow parsing and validation of input to be completed before the beginning of the simulation proper, i.e. fail fast conserve HPC resources.
Simulation objects take valid Input objects as constructor arguments.
Refactor to a situation where a one to one relationship holds between a given input node and a consuming input object.
The Input class for a particular Simulation class should be data structure containing native data type members corresponding to a read only representation of user input need to instantiate a valid Simulation object.
Simulation objects will be required to be valid at construction whenever possible.
Existing pool objects should also be taken as constructor arguements.
The Input object is the single source of truth for input parameters.
The Simulation class should aggregate the Input class.
Access to input values should be through the aggregated Input.
Only values that are derived at simulation time by transformation of input values should be stored in the Simulation object itself.
Values that are calculated using only input values should be calculated and stored as derived values in the Input object.
Where a Simulation object requires input parameters from another simulation object, carefully consider lifetimes, and on case by case basis decide whether the simulation object, a more restricted type, or an input object to be taken as a constructor argument.
A base class
InputSectionallowing the specification of the user input and handling most parsing of the XML input is provided.Input classes compose one or more types derived from
InputSection. The basic class hierarchy this results in is illustrated in (see Fig. 30).
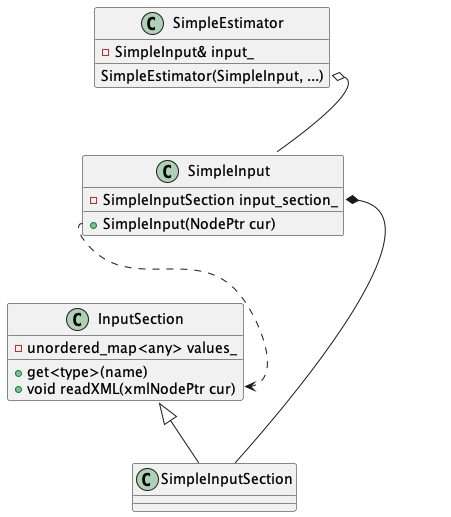
Fig. 30 “Modern” input scheme low level class diagram. Simulation class SimpleSimObject, takes input class SimpleInput as a constructor argument, in general sharing a aggregate relationship. SimpleInput composes an input section class SimpleInputSection derived from InputSection base class. SimpleInput gains input parsing functionality from SimpleInputSection.
The
InputSectionclass parses the string representations of input data that have been previously organized hierarchically within Libxml2 data structures.Input values of are stored in a single hash table where strongly typed polymorphism is supported by
std::any.The parsed inputs are checked for type and name validity.
Subtypes are expected to implement specific input validation by overriding the
InputSection::checkParticularValidityvirtual method.
How to use the improved input design
Determine for your simulation object what are the immutable parameters that are read from or directly derived from user input. These will be the data members of the input class.
If your simulation class is called
MySimObjectname the input classMySimObjectInput.- Add a constructor that takes an xmlNodePtr as an argument. - Add data members for each element of the input. - Use appropriate data types, if an input is a “position” using a typePositionin the Simulation class, then it should be parsed, translated to, stored as and if possible checked to be valid by the Input class. Don’t store it as a string and do further parsing in the simulation class!Derive a class from
InputSectionand add it to yourMySimObjectInputclass. Here we’ll call itMySimObjectInputSectionDefine your user input in
MySimObjectInputSection’s default constructor.
Default the copy constructor. (This is to allow parent Input classes to include this Input class in std::variants of their delegate classes)
Add a private data member for the your input section to
MySimObjectInputcall itinput_section_Make an implementation file if you have not,
MySimObjectInput.cpp.In your
MySimObjectInput::MySimObjectInput(xmlNodePtr& cur)callinput_section_.readXML(cur)to parse input.In your constructor use the
LAMBDA_setIfInInputmacro to copyMyInputSectionvariables if read to your native data members. (Listing 86), the macro generated lambda is strongly typed.
class MySimObjectInput
{
MySimObjectInput() {
input_section_.readXML(cur);
auto setIfInInput = LAMBDA_setIfInInput;
setIfInInput(energy_matrix_, "energy_matrix");
...
}
};
Write unit tests
tests/test_MySimObjectInput.cppseesrc/Estimators/test_OneBodyDensityMatricesInput.cpp
Declaring input node Contents
The constructor of the InputSection subtype uses a pseudo DSL to define the input node the section handles. Doing this lets InputSection know what type difference input parameters and attributes must be as well as what is expected, optional, and what doesn’t belong in the input node at all.
class TestInputSection : public InputSection
{
public:
TestInputSection()
{
section_name = "Test";
attributes = {"name", "samples", "kmax", "full"};
parameters = {"label", "count", "width", "rational", "testenum1",
"testenum2", "sposets", "center", "density", "target"};
required = {"count", "full"};
strings = {"name", "label"};
multi_strings = {"sposets"};
multi_reals = {"density"};
multiple = {"target"};
integers = {"samples", "count"};
reals = {"kmax", "width"};
positions = {"center", "target"};
bools = {"full", "rational"};
enums = {"testenum1", "testenum2"};
default_values = {{"name", std::string("demo")},
{"samples", int(20)},
{"width", Real(1.0)},
{"rational", bool(false)}};
}
}
Any easy way of thinking about this is you are adding your input elements to different logical sets from parsing and validation. The input breaks down into attributes and parameters for each node. So first each element is added to one of these two sets. Then required inputs should be added to the required set. If its permissible for multiple instances of an input element in the section add it to the multiples set. Then each element should be added to the type set it matches. The types supported are: strings, bools, integers, reals, positions, multi_strings, multi_reals. Two require special mention, multi_strings and multi_reals parse multiple whitespace separated values to a vector of strings or reals. If your type has a fixed number of values and you define and element as one of these types you should validate you have parsed the expected number of values in your input section subtype’s checkParticularValidbity.
Without extension InputSection provides only a basic set of types and expects only attribute and parameter elements. There is an established API for delegation to other input classes when an included child nodes are actually complex Inputs in their own right, i.e. not just parameters and attribute. There is also an extension method through custom stream handlers for types not covered by InputSection (see _advanced-input_section). Any element of input that isn’t declared in this fashion will cause a fatal error when the input node is parsed by the InputSection.
Special concerns if your InputClass is for an Estimator
Estimators are runtime selected simulation objects managed by the EstimatorManagerNew and their inputs are similarly handled by the EstimatorManagerInput object. The EstimatorManagerInput delegates particular child nodes of input at runtime to a compile time known set of input classes. Your class will be one, lets assume its named MyEstimator.
This requires that in addition to creating and unit testing MyEstimatorInput as explained above, you will also need to integrate it with EstimatorManagerInput, its’ parent in the native input structure of QMCPACK.
Add your input class header
MyEstimatorInput.htoEstimatorInputDelegates.h, this makes its definition visible to compilation units that need to be able to useEstimatorInputas a complete type.
Warning
Do not include EstimatorInputDelegates.h file in MyEstimatorInput.cpp or MyEstimator.cpp include MyEstimatorInput.h directly.
Add your
MyEstimatorClassto theEstimatorInputstd::variant in inEstimatorManagerInput.hIn
EstimatorManagerInput::readXMLadd a case that connects the estimator type tag your estimator uses to itsMyEstimatorInput.
else if (atype == "perparticlehamiltonianlogger")
appendEstimatorInput<PerParticleHamiltonianLoggerInput>(child);
// Your new code
else if (atype == "myestimator")
appendEstimatorInput<MyEstimatorInput>(child);
Add a valid input section for your input class to the integration testing in
tests/test_EstimatorManagerInput.cpp
Advanced Features of InputSection
Delegation to InputClasses
This is used when child node in input represents another logical input class we register a factory function for that input child class as a delegate of the input class responsible for the parent node.
The delgating class should will pass an entire node to this input class factory function and receive an input class as a
std::anyback. The delegate class is expected to take responsibility for complete parsing of this node. Including its own internal validation. a tag name (see Delgating to another InputSection subtype).
/** Generic delgate input class.
* The delegate input requires:
* A constructor that takes an xmlNodePtr
* A factoryFunction that matches the signature discussed in InputSection::DelegateHandler
*/
class AnotherInput
{
public:
class AnotherInputSection : public InputSection
{
...
};
AnotherInput(xmlNodePtr cur)
{
...
}
};
/// Factory function for the delegate Input class.
std::any makeAnotherInput(xmlNodePtr cur, std::string& value_label)
{
AnotherInput another_input{cur};
value_label = another_input.get_name();
return another_input;
}
/** Input class delegating to other input classes.
*/
class DelegatingInput
{
class DelegatingInputSection : public InputSection
{
public:
DelegatingInputSection()
{
section_name = "DelegateTest";
...
delegates = {"anotherinput"};
InputSection::registerDelegate("anotherinput", makeAnotherInput);
}
};
public:
DelegatingInput(xmlNodePtr cur) { dins_.readXML(cur); }
// rather than write a real input class we just pass through InputSection for this test.
bool has(const std::string& name) const { return dins_.has(name); }
template<typename T>
T get(const std::string& name) const
{
return dins_.get<T>(name);
}
private:
std::string name_ = "DelegatingInput";
DelegatingInputSection dins_;
};
Custom stream handlers
In the case that we just have a input parameter that is unique to a particular input class, not for one of the types handled by InputSection, and it does not logically map to a separate Input we should use a custom stream handler (see Implementing a custom type handler for an Input class.).
class CustomTypeInput : public InputSection
{
public:
struct LabeledPosition
{
std::string letters;
std::array<int, 3> numbers;
};
CustomTestInput()
{
...
attributes = {"name", "custom_attribute"};
custom = {"labeled_position", "custom_attribute"};
}
void setFromStreamCustom(const std::string& ename, const std::string& name, std::istringstream& svalue) override
{
if (ename == "labeled_position")
{
LabeledPosition ws;
svalue >> ws.letters;
svalue >> ws.numbers[0];
svalue >> ws.numbers[1];
svalue >> ws.numbers[2];
values_[name] = ws;
}
else if (name == "custom_attribute")
{
std::string cus_at;
// otherwise you will get not consume the entire attribute just the next piece as determine by operator>> and
// the type you are going into.
std::getline(svalue, cus_at);
... // do your custom parsing.
values_[name] = cus_at;
}
else
throw std::runtime_error("bad name passed: " + name +
" or custom setFromStream not implemented in derived class.");
}
};
Particles and distance tables
ParticleSets
The ParticleSet class stores particle positions and attributes
(charge, mass, etc).
The R member stores positions. For calculations, the R variable
needs to be transferred to the structure-of-arrays (SoA) storage in
RSoA. This is done by the update method. In the future the
interface may change to use functions to set and retrieve positions so
the SoA transformation of the particle data can happen automatically.
For now, it is crucial to call P.update() to populate RSoA anytime P.R is changed. Otherwise, the distance tables associated with R will be uninitialized or out-of-date.
const SimulationCell sc;
ParticleSet elec(sc), ions(sc);
elec.setName("e");
ions.setName("ion0");
// initialize ions
ions.create({2});
ions.R[0] = {0.0, 0.0, 0.0};
ions.R[1] = {0.5, 0.5, 0.5};
ions.update(); // transfer to RSoA
// initialize elec
elec.create({1,1});
elec.R[0] = {0.0, 0.0, 0.0};
elec.R[1] = {0.0, 0.25, 0.0};
const int itab = elec.addTable(ions);
elec.update(); // update RSoA and distance tables
// d_table is an electron-ion distance table
const auto& d_table = elec.getDistTableAB(itab);
A particular distance table is retrieved with getDistTable. Use
addTable to add a ParticleSet and return the index of the
distance table. If the table already exists the index of the existing
table will be returned.
The mass and charge of each particle is stored in Mass and Z.
The flag, SameMass, indicates if all the particles have the same
mass (true for electrons).
Groups
Particles can belong to different groups. For electrons, the groups are
up and down spins. For ions, the groups are the atomic elements. The
group type for each particle can be accessed through the GroupID
member. The number of groups is returned from groups(). The total
number particles is accessed with getTotalNum(). The number of
particles in a group is groupsize(int igroup).
The particle indices for each group are found with first(int igroup)
and last(int igroup).
Distance tables
Distance tables store distances between particles. There are symmetric (AA) tables for distance between like particles (electron-electron or ion-ion) and asymmetric (AB) tables for distance between unlike particles (electron-ion)
The Distances and Displacements members contain the data. The
indexing order is target index first, then source. For electron-ion
tables, the sources are the ions and the targets are the electrons.
Looping over particles
Some sample code on how to loop over all the particles in an electron-ion distance table:
// d_table is an electron-ion distance table
for (int jat = 0; j < d_table.targets(); jat++) { // Loop over electrons
for (int iat = 0; i < d_table.sources(); iat++) { // Loop over ions
d_table.Distances[jat][iat];
}
}
Interactions sometimes depend on the type of group of the particles. The
code can loop over all particles and use GroupID[idx] to choose the
interaction. Alternately, the code can loop over the number of groups
and then loop from the first to last index for those groups. This method
can attain higher performance by effectively hoisting tests for group ID
out of the loop.
An example of the first approach is
// P is a ParticleSet
for (int iat = 0; iat < P.getTotalNum(); iat++) {
int group_idx = P.GroupID[iat];
// Code that depends on the group index
}
An example of the second approach is
// P is a ParticleSet
assert(P.IsGrouped == true); // ensure particles are grouped
for (int ig = 0; ig < P.groups(); ig++) { // loop over groups
for (int iat = P.first(ig); iat < P.last(ig); iat++) { // loop over elements in each group
// Code that depends on group
}
}
Wavefunction
A full TrialWaveFunction is formulated as a product
of all the components. Each component derives from WaveFunctionComponent.
QMCPACK doesn’t directly use the product form but mostly uses the log of the wavefunction. It is a natural fit for QMC algorithms and offers a numerical advantage on computers. The log value grows linearly instead of exponentially, beyond the range of double precision, with respect to the electron counts in a Slater-Jastrow wave function.
The code contains an example of a wavefunction component for a Helium atom using a simple form and is described in Helium Wavefunction Example
Mathematical preliminaries
The wavefunction evaluation functions compute the log of the wavefunction, the gradient and the Laplacian of the log of the wavefunction. Expanded, the gradient and Laplacian are
where \(i\) is the electron index.
In this separable form, each wavefunction component computes its \({\bf \tilde G}\) WaveFunctionComponent::G and \({\bf \tilde L}\) WaveFunctionComponent::L. The sum over components are stored in TrialWaveFunction::G and TrialWaveFunction::L.
The \(\frac{{\nabla ^2} \psi}{\psi}\) needed by kinetic part of the local energy can be computed as
see QMCHamiltonians/BareKineticEnergy.h.
Wavefunction evaluation
The process for creating a new wavefunction component class is to derive from WaveFunctionComponent and implement a number pure virtual functions. To start most of them can be empty.
The following four functions evaluate the wavefunction values and spatial derivatives:
evaluateLog Computes the log of the wavefunction and the gradient
and Laplacian (of the log of the wavefunction) for all particles. The
input is theParticleSet(P) (of the electrons). The log of
the wavefunction should be stored in the LogValue member variable,
and used as the return value from the function. The gradient is stored
in G and the Laplacian in L.
ratio Computes the wavefunction ratio (not the log) for a single
particle move (\(\psi_{new}/\psi_{old}\)). The inputs are the
ParticleSet(P) and the particle index (iat).
evalGrad Computes the gradient for a given particle. The inputs are
the ParticleSet(P) and the particle index (iat).
ratioGrad Computes the wavefunction ratio and the gradient at the
new position for a single particle move. The inputs are the
ParticleSet(P) and the particle index (iat). The output
gradient is in grad_iat;
The updateBuffer function needs to be implemented, but to start it
can simply call evaluateLog.
The put function should be implemented to read parameter specifics
from the input XML file.
Function use
For debugging it can be helpful to know the under what conditions the various routines are called.
The VMC and DMC loops initialize the walkers by calling evaluateLog.
For all-electron moves, each timestep advance calls evaluateLog. If
the use_drift parameter is no, then only the wavefunction value is
used for sampling. The gradient and Laplacian are used for computing the
local energy.
For particle-by-particle moves, each timestep advance
calls
evalGradcomputes a trial move
calls
ratioGradfor the wavefunction ratio and the gradient at the trial position. (If theuse_driftparameter is no, theratiofunction is called instead.)
The following example shows part of an input block for VMC with all-electron moves and drift.
<qmc method="vmc" target="e" move="alle">
<parameter name="use_drift">yes</parameter>
</qmc>
Particle distances
The ParticleSet parameter in these functions refers to the
electrons. The distance tables that store the inter-particle distances
are stored as an array.
To get the electron-ion distances, add the ion ParticleSet using
addTable and save the returned index. Use that index to get the
ion-electron distance table.
const int ei_id = elecs.addTable(ions); // in the constructor only
const auto& ei_table = elecs.getDistTable(ei_id); // when consuming a distance table
Getting the electron-electron distances is very similar, just add the
electron ParticleSet using addTable.
Only the lower triangle for the electron-electron table should be used. It is the only part of the distance table valid throughout the run. During particle-by-particle move, there are extra restrictions. When a move of electron iel is proposed, only the lower triangle parts [0,iel)[0,iel) [iel, Nelec)[iel, Nelec) and the row [iel][0:Nelec) are valid. In fact, the current implementation of distance based two and three body Jastrow factors in QMCPACK only needs the row [iel][0:Nelec).
In ratioGrad, the new distances are stored in the Temp_r and
Temp_dr members of the distance tables.
Legacy Setup
Warning
The following describes a deprecated method of handling user input. It is not to be used for new code.
A builder processes XML input, creates the wavefunction, and adds it to
targetPsi. Builders derive from WaveFunctionComponentBuilder.
The new builder hooks into the XML processing in
WaveFunctionFactory.cpp in the build function.
Caching values
The acceptMove and restore methods are called on accepted and
rejected moves for the component to update cached values.
Threading
The makeClone function needs to be implemented to work correctly
with OpenMP threading. There will be one copy of the component created
for each thread. If there is no extra storage, calling the copy
constructor will be sufficient. If there are cached values, the clone
call may need to create space.
Parameter optimization
The checkInVariables, checkOutVariables, and resetParameters
functions manage the variational parameters. Optimizable variables also
need to be registered when the XML is processed.
Variational parameter derivatives are computed in the
evaluateDerivatives function. It computes the derivatives of both the log
of the wavefunction and kinetic energy with respect to optimizable parameters
and adds the results to the corresponding output arrays.
The kinetic energy derivatives are computed as
with each WaveFunctionComponent contributing
Right now \(1/m\) factor is applied in TrialWaveFunction.
This is a bug when the particle set doesn’t hold equal mass particles.
Helium Wavefunction Example
The code contains an example of a wavefunction component for a Helium atom using STO orbitals and a Pade Jastrow.
to The wavefunction is
where \(Z = 2\) is the nuclear charge, \(A=1/2\) is the
electron-electron cusp, and \(B\) is a variational parameter. The
electron-ion distances are \(r_1\) and \(r_2\), and
\(r_{12}\) is the electron-electron distance. The wavefunction is
the same as the one expressed with built-in components in
examples/molecules/He/he_simple_opt.xml.
The code is in src/QMCWaveFunctions/ExampleHeComponent.cpp. The
builder is in src/QMCWaveFunctions/ExampleHeBuilder.cpp. The input
file is in examples/molecules/He/he_example_wf.xml. A unit test
compares results from the wavefunction evaluation functions for
consistency in src/QMCWaveFunctions/tests/test_example_he.cpp.
The recommended approach for creating a new wavefunction component is to copy the example and the unit test. Implement the evaluation functions and ensure the unit test passes.
Linear Algebra
Like in many methods which solve the Schrödinger equation, linear algebra plays a critical role in QMC algorithms and thus is crucial to the performance of QMCPACK. There are a few components in QMCPACK use BLAS/LAPACK with their own characteristics.
Real space QMC
Single particle orbitals
Spline evaluation as commonly used in solid-state simulations does not use any dense linear algebra library calls. LCAO evaluation as commonly used in molecular calculations relies on BLAS2 GEMV to compute SPOs from a basis set.
Slater determinants
Slater determinants are calculated on \(N \times N\) Slater matrices. \(N\) is the number of electrons for a given spin. In the actually implementation, operations on the inverse matrix of Slater matrix for each walker dominate the computation. To initialize it, DGETRF and DGETRI from LAPACK are called. The inverse matrix can be stored out of place. During random walking, inverse matrices are updated by either Sherman-Morrison rank-1 update or delayed update. Update algorithms heavily relies on BLAS. All the BLAS operations require S,C,D,Z cases.
Sherman-Morrison rank-1 update uses BLAS2 GEMV and GER on \(N \times N\) matrices.
Delayed rank-K update uses
BLAS1 SCOPY on \(N\) array.
BLAS2 GEMV, GER on \(k \times N\) and \(k \times k\) matrices. \(k\) ranges from 1 to \(K\) when updates are delayed and accumulated.
BLAS3 GEMM at the final update.
’T’, ’N’, K, N, N
’N’, ’N’, N, K, K
’N’, ’N’, N, N, K
The optimal K depends on the hardware but it usually ranges from 32 to 256.
QMCPACK solves systems with a few to thousands of electrons. To make all the BLAS/LAPACK operation efficient on accelerators. Batching is needed and optimized for \(N < 2000\). Non-batched functions needs to be optimized for \(N > 500\). Note: 2000 and 500 are only rough estimates.
Wavefunction optimizer
to be added.
Auxiliary field QMC
The AFQMC implementation in QMCPACK relies heavily on linear algebra operations from BLAS/LAPACK. The performance of the code is netirely dependent on the performance of these libraries. See below for a detailed list of the main routines used from BLAS/LAPACK. Since the AFQMC code can work with both single and double precision builds, all 4 versions of these routines (S,C,D,Z) are generally needed, for this reason we omit the data type label.
BLAS1: SCAL, COPY, DOT, AXPY
BLAS2: GEMV, GER
BLAS3: GEMM
LAPACK: GETRF, GETRI, GELQF, UNGLQ, ORGLQ, GESVD, HEEVR, HEGVX
While the dimensions of the matrix operations will depend entirely on the details of the calculation, typical matrix dimensions range from the 100s, for small system sizes, to over 20000 for the largest calculations attempted so far. For builds with GPU accelerators, we make use of batched and strided implementations of these routines. Batched implementations of GEMM, GETRF, GETRI, GELQF and UNGLQ are particularly important for the performance of the GPU build on small to medium size problems. Batched implementations of DOT, AXPY and GEMV would also be quite useful, but they are not yet generally available. On GPU builds, the code uses batched implementations of these routines when available by default.
Slater-backflow wavefunction implementation details
For simplicity, consider \(N\) identical fermions of the same spin (e.g., up electrons) at spatial locations \(\{\mathbf{r}_1,\mathbf{r}_2,\dots,\mathbf{r}_{N}\}\). Then the Slater determinant can be written as
where each entry in the determinant is an SPO evaluated at a particle position
When backflow transformation is applied to the determinant, the particle coordinates \(\mathbf{r}_i\) that go into the SPOs are replaced by quasi-particle coordinates \(\mathbf{x}_i\):
where
\(r_{ij}=\vert\mathbf{r}_i-\mathbf{r}_j\vert\). The integers i,j label the particle/quasi-particle. There is a one-to-one correspondence between the particles and the quasi-particles, which is simplest when \(\eta=0\).
Value
The evaluation of the Slater-backflow wavefunction is almost identical
to that of a Slater wavefunction. The only difference is that the
quasi-particle coordinates are used to evaluate the SPOs. The actual
value of the determinant is stored during the inversion of the matrix
\(M\) (cgetrf\(\rightarrow\)cgetri). Suppose
\(M=LU\), then \(S=\prod\limits_{i=1}^N L_{ii} U_{ii}\).
// In DiracDeterminantWithBackflow::evaluateLog(P,G,L)
Phi->evaluate(BFTrans->QP, FirstIndex, LastIndex, psiM,dpsiM,grad_grad_psiM);
psiMinv = psiM;
LogValue=InvertWithLog(psiMinv.data(),NumPtcls,NumOrbitals
,WorkSpace.data(),Pivot.data(),PhaseValue);
QMCPACK represents the complex value of the wavefunction in polar
coordinates \(S=e^Ue^{i\theta}\). Specifically, LogValue
\(U\) and PhaseValue \(\theta\) are handled separately. In
the following, we will consider derivatives of the log value only.
Gradient
To evaluate particle gradient of the log value of the Slater-backflow wavefunction, we can use the \(\log\det\) identity in (261). This identity maps the derivative of \(\log\det M\) with respect to a real variable \(p\) to a trace over \(M^{-1}dM\):
Following Kwon, Ceperley, and Martin [KCM93], the particle gradient
where the quasi-particle gradient matrix
and the intermediate matrix
with the SPO derivatives (w.r. to quasi-particle coordinates)
Notice that we have made the name change of \(\phi\rightarrow M\)
from the notations of ref. [KCM93]. This
name change is intended to help the reader associate M with the QMCPACK
variable psiM.
// In DiracDeterminantWithBackflow::evaluateLog(P,G,L)
for(int i=0; i<num; i++) // k in above formula
{
for(int j=0; j<NumPtcls; j++)
{
for(int k=0; k<OHMMS_DIM; k++) // alpha in above formula
{
myG(i) += dot(BFTrans->Amat(i,FirstIndex+j),Fmat(j,j));
}
}
}
(262) is still relatively simple to understand. The \(A\) matrix maps changes in particle coordinates \(d\mathbf{r}\) to changes in quasi-particle coordinates \(d\mathbf{x}\). Dotting A into F propagates \(d\mathbf{x}\) to \(dM\). Thus \(F\cdot A\) is the term inside the trace operator of (261). Finally, performing the trace completes the evaluation of the derivative.
Laplacian
The particle Laplacian is given in [KCM93] as
where the quasi-particle Laplacian matrix
with the second derivatives of the single-particles orbitals being
Schematically, \(L_i\) has contributions from three terms of the form \(BF, AAFF, and tr(AA,Md2M)\), respectively. \(A, B, M ,d2M,\) and \(F\) can be calculated and stored before the calculations of \(L_i\). The first \(BF\) term can be directly calculated in a loop over quasi-particle coordinates \(j\alpha\).
// In DiracDeterminantWithBackflow::evaluateLog(P,G,L)
for(int j=0; j<NumPtcls; j++)
for(int a=0; a<OHMMS_DIM; k++)
myL(i) += BFTrans->Bmat_full(i,FirstIndex+j)[a]*Fmat(j,j)[a];
Notice that \(B_{ij}^\alpha\) is stored in Bmat_full, NOT
Bmat.
The remaining two terms both involve \(AA\). Thus, it is best to define a temporary tensor \(AA\):
which we will overwrite for each particle \(i\). Similarly, define \(FF\):
which is simply the outer product of \(F\otimes F\). Then the \(AAFF\) term can be calculated by fully contracting \(AA\) with \(FF\).
// In DiracDeterminantWithBackflow::evaluateLog(P,G,L)
for(int j=0; j<NumPtcls; j++)
for(int k=0; k<NumPtcls; k++)
for(int i=0; i<num; i++)
{
Tensor<RealType,OHMMS_DIM> AA = dot(transpose(BFTrans->Amat(i,FirstIndex+j)),BFTrans->Amat(i,FirstIndex+k));
HessType FF = outerProduct(Fmat(k,j),Fmat(j,k));
myL(i) -= traceAtB(AA,FF);
}
Finally, define the SPO derivative term:
then the last term is given by the contraction of \(Md2M\) (q_j)
with the diagonal of \(AA\).
for(int j=0; j<NumPtcls; j++)
{
HessType q_j;
q_j=0.0;
for(int k=0; k<NumPtcls; k++)
q_j += psiMinv(j,k)*grad_grad_psiM(j,k);
for(int i=0; i<num; i++)
{
Tensor<RealType,OHMMS_DIM> AA = dot(
transpose(BFTrans->Amat(i,FirstIndex+j)),
BFTrans->Amat(i,FirstIndex+j)
);
myL(i) += traceAtB(AA,q_j);
}
}
Wavefunction parameter derivative
To use the robust linear optimization method of [TU07], the trial wavefunction needs to know its contributions to the overlap and hamiltonian matrices. In particular, we need derivatives of these matrices with respect to wavefunction parameters. As a consequence, the wavefunction \(\psi\) needs to be able to evaluate \(\frac{\partial}{\partial p} \ln \psi\) and \(\frac{\partial}{\partial p} \frac{\mathcal{H}\psi}{\psi}\), where \(p\) is a parameter.
When 2-body backflow is considered, a wavefunction parameter \(p\) enters the \(\eta\) function only (equation (260)). \(\mathbf{r}\), \(\phi\), and \(M\) do not explicitly dependent on \(p\). Derivative of the log value is almost identical to particle gradient. Namely, (262) applies upon the substitution \(r_i^\alpha\rightarrow p\).
where the quasi-particle derivatives are stored in Cmat
The change in local kinetic energy is a lot more difficult to calculate
where \(L_i\) is the particle Laplacian defined in (266) To evaluate (274), we need to calculate parameter derivatives of all three terms defined in the Laplacian evaluation. Namely \((B)(F)\), \((AA)(FF)\), and \(\text{tr}(AA,Md2M)\), where we have put parentheses around previously identified data structures. After \(\frac{\partial}{\partial p}\) hits, each of the three terms will split into two terms by the product rule. Each smaller term will contain a contraction of two data structures. Therefore, we will need to calculate the parameter derivatives of each data structure defined in the Laplacian evaluation:
X and Y are stored as Xmat and Ymat_full (NOT Ymat) in the
code. dF is dFa. \(AA'\) is not fully stored; intermediate
values are stored in Aij_sum and a_j_sum. \(FF'\) is
calculated on the fly as \(dF\otimes F+F\otimes dF\). \(Md2M'\)
is not stored; intermediate values are stored in q_j_prime.
Scalar estimator implementation
Introduction: Life of a specialized OperatorBase
Almost all observables in QMCPACK are implemented as specialized derived classes of the OperatorBase base class. Each observable is instantiated in HamiltonianFactory and added to QMCHamiltonian for tracking. QMCHamiltonian tracks two types of observables: main and auxiliary. Main observables contribute to the local energy. These observables are elements of the simulated Hamiltonian such as kinetic or potential energy. Auxiliary observables are expectation values of matrix elements that do not contribute to the local energy. These Hamiltonians do not affect the dynamics of the simulation. In the code, the main observables are labeled by “physical” flag; the auxiliary observables have“physical” set to false.
Initialization
When an <estimator type="est_type" name="est_name" other_stuff="value"/> tag is present in the <hamiltonian/> section, it is first read by HamiltonianFactory. In general, the type of the estimator will determine which specialization of OperatorBase should be instantiated, and a derived class with myName="est_name" will be constructed. Then, the put() method of this specific class will be called to read any other parameters in the <estimator/> XML node. Sometimes these parameters will instead be read by HamiltonianFactory because it can access more objects than OperatorBase.
Cloning
When OpenMP threads are spawned, the estimator will be cloned by the CloneManager, which is a parent class of many QMC drivers.
// In CloneManager.cpp
#pragma omp parallel for shared(w,psi,ham)
for(int ip=1; ip<NumThreads; ++ip)
{
wClones[ip]=new MCWalkerConfiguration(w);
psiClones[ip]=psi.makeClone(*wClones[ip]);
hClones[ip]=ham.makeClone(*wClones[ip],*psiClones[ip]);
}
In the preceding snippet, ham is the reference to the estimator on the master thread. If the implemented estimator does not allocate memory for any array, then the default constructor should suffice for the makeClone method.
// In SpeciesKineticEnergy.cpp
OperatorBase* SpeciesKineticEnergy::makeClone(ParticleSet& qp, TrialWaveFunction& psi)
{
return new SpeciesKineticEnergy(*this);
}
If memory is allocated during estimator construction (usually when parsing the XML node in the put method), then the makeClone method should perform the same initialization on each thread.
OperatorBase* LatticeDeviationEstimator::makeClone(ParticleSet& qp, TrialWaveFunction& psi)
{
LatticeDeviationEstimator* myclone = new LatticeDeviationEstimator(qp,spset,tgroup,sgroup);
myclone->put(input_xml);
return myclone;
}
Evaluate
After the observable class (derived class of OperatorBase) is constructed and prepared (by the put() method), it is ready to be used in a QMCDriver. A QMCDriver will call H.auxHevaluate(W,thisWalker) after every accepted move, where H is the QMCHamiltonian that holds all main and auxiliary Hamiltonian elements, W is a MCWalkerConfiguration, and thisWalker is a pointer to the current walker being worked on. As shown in the following, this function goes through each auxiliary Hamiltonian element and evaluates it using the current walker configuration. Under the hood, observables are calculated and dumped to the main particle set’s property list for later collection.
// In QMCHamiltonian.cpp
// This is more efficient.
// Only calculate auxH elements if moves are accepted.
void QMCHamiltonian::auxHevaluate(ParticleSet& P, Walker_t& ThisWalker)
{
#if !defined(REMOVE_TRACEMANAGER)
collect_walker_traces(ThisWalker,P.current_step);
#endif
for(int i=0; i<auxH.size(); ++i)
{
auxH[i]->setHistories(ThisWalker);
RealType sink = auxH[i]->evaluate(P);
auxH[i]->setObservables(Observables);
#if !defined(REMOVE_TRACEMANAGER)
auxH[i]->collect_scalar_traces();
#endif
auxH[i]->setParticlePropertyList(P.PropertyList,myIndex);
}
}
For estimators that contribute to the local energy (main observables), the return value of evaluate() is used in accumulating the local energy. For auxiliary estimators, the return value is not used (sink local variable above); only the value of Value is recorded property lists by the setObservables() method as shown in the preceding code snippet. By default, the setObservables() method will transfer auxH[i]->Value to P.PropertyList[auxH[i]->myIndex]. The same property list is also kept by the particle set being moved by QMCDriver. This list is updated by auxH[i]->setParticlePropertyList(P.PropertyList,myIndex), where myIndex is the starting index of space allocated to this specific auxiliary Hamiltonian in the property list kept by the target particle set P.
Collection
The actual statistics are collected within the QMCDriver, which owns an EstimatorManager object. This object (or a clone in the case of multithreading) will be registered with each mover it owns. For each mover (such as VMCUpdatePbyP derived from QMCUpdateBase), an accumulate() call is made, which by default, makes an accumulate(walkerset) call to the EstimatorManager it owns. Since each walker has a property set, EstimatorManager uses that local copy to calculate statistics. The EstimatorManager performs block averaging and file I/O.
Single scalar estimator implementation guide
Almost all of the defaults can be used for a single scalar observable. With any luck, only the put() and evaluate() methods need to be implemented. As an example, this section presents a step-by-step guide for implementing a verb|SpeciesKineticEnergy| estimator that calculates the kinetic energy of a specific species instead of the entire particle set. For example, a possible input to this estimator can be:
<estimator type="specieskinetic" name="ukinetic" group="u"/>
<estimator type="specieskinetic" name="dkinetic" group="d"/>.
This should create two extra columns in the scalar.dat file that contains the kinetic energy of the up and down electrons in two separate columns. If the estimator is properly implemented, then the sum of these two columns should be equal to the default Kinetic column.
Barebone
The first step is to create a barebone class structure for this simple scalar estimator. The goal is to be able to instantiate this scalar estimator with an XML node and have it print out a column of zeros in the scalar.dat file.
To achieve this, first create a header file “SpeciesKineticEnergy.h” in the QMCHamiltonians folder, with only the required functions declared as follows:
// In SpeciesKineticEnergy.h
#ifndef QMCPLUSPLUS_SPECIESKINETICENERGY_H
#define QMCPLUSPLUS_SPECIESKINETICENERGY_H
#include <Particle/WalkerSetRef.h>
#include <QMCHamiltonians/OperatorBase.h>
namespace qmcplusplus
{
class SpeciesKineticEnergy: public OperatorBase
{
public:
SpeciesKineticEnergy(ParticleSet& P):tpset(P){ };
bool put(xmlNodePtr cur); // read input xml node, required
bool get(std::ostream& os) const; // class description, required
Return_t evaluate(ParticleSet& P);
inline Return_t evaluate(ParticleSet& P, std::vector<NonLocalData>& Txy)
{ // delegate responsity inline for speed
return evaluate(P);
}
// pure virtual functions require overrider
void resetTargetParticleSet(ParticleSet& P) { } // required
OperatorBase* makeClone(ParticleSet& qp, TrialWaveFunction& psi); // required
private:
ParticleSet& tpset;
}; // SpeciesKineticEnergy
} // namespace qmcplusplus
#endif
Notice that a local reference tpset to the target particle set P is saved in the constructor. The target particle set carries much information useful for calculating observables. Next, make “SpeciesKineticEnergy.cpp,” and make vacuous definitions.
// In SpeciesKineticEnergy.cpp
#include <QMCHamiltonians/SpeciesKineticEnergy.h>
namespace qmcplusplus
{
bool SpeciesKineticEnergy::put(xmlNodePtr cur)
{
return true;
}
bool SpeciesKineticEnergy::get(std::ostream& os) const
{
return true;
}
SpeciesKineticEnergy::Return_t SpeciesKineticEnergy::evaluate(ParticleSet& P)
{
Value = 0.0;
return Value;
}
OperatorBase* SpeciesKineticEnergy::makeClone(ParticleSet& qp, TrialWaveFunction& psi)
{
// no local array allocated, default constructor should be enough
return new SpeciesKineticEnergy(*this);
}
} // namespace qmcplusplus
Now, head over to HamiltonianFactory and instantiate this observable if an XML node is found requesting it. Look for “gofr” in HamiltonianFactory.cpp, for example, and follow the if block.
// In HamiltonianFactory.cpp
#include <QMCHamiltonians/SpeciesKineticEnergy.h>
else if(potType =="specieskinetic")
{
SpeciesKineticEnergy* apot = new SpeciesKineticEnergy(*target_particle_set);
apot->put(cur);
targetH->addOperator(apot,potName,false);
}
The last argument of addOperator() (i.e., the false flag) is crucial. This tells QMCPACK that the observable we implemented is not a physical Hamiltonian; thus, it will not contribute to the local energy. Changes to the local energy will alter the dynamics of the simulation. Finally, add “SpeciesKineticEnergy.cpp” to HAMSRCS in “CMakeLists.txt” located in the QMCHamiltonians folder. Now, recompile QMCPACK and run it on an input that requests <estimator type="specieskinetic" name="ukinetic"/> in the hamiltonian block. A column of zeros should appear in the scalar.dat file under the name “ukinetic.”
Evaluate
The evaluate() method is where we perform the calculation of the desired observable. In a first iteration, we will simply hard-code the name and mass of the particles.
// In SpeciesKineticEnergy.cpp
#include <QMCHamiltonians/BareKineticEnergy.h> // laplaician() defined here
SpeciesKineticEnergy::Return_t SpeciesKineticEnergy::evaluate(ParticleSet& P)
{
std::string group="u";
RealType minus_over_2m = -0.5;
SpeciesSet& tspecies(P.getSpeciesSet());
Value = 0.0;
for (int iat=0; iat<P.getTotalNum(); iat++)
{
if (tspecies.speciesName[ P.GroupID(iat) ] == group)
{
Value += minus_over_2m*laplacian(P.G[iat],P.L[iat]);
}
}
return Value;
// Kinetic column has:
// Value = -0.5*( Dot(P.G,P.G) + Sum(P.L) );
}
Voila—you should now be able to compile QMCPACK, rerun, and see that the values in the “ukinetic” column are no longer zero. Now, the only task left to make this basic observable complete is to read in the extra parameters instead of hard-coding them.
Parse extra input
The preferred method to parse extra input parameters in the XML node is to implement the put() function of our specific observable. Suppose we wish to read in a single string that tells us whether to record the kinetic energy of the up electron (group=“u”) or the down electron (group=“d”). This is easily achievable using the OhmmsAttributeSet class,
// In SpeciesKineticEnergy.cpp
#include <OhmmsData/AttributeSet.h>
bool SpeciesKineticEnergy::put(xmlNodePtr cur)
{
// read in extra parameter "group"
OhmmsAttributeSet attrib;
attrib.add(group,"group");
attrib.put(cur);
// save mass of specified group of particles
SpeciesSet& tspecies(tpset.getSpeciesSet());
int group_id = tspecies.findSpecies(group);
int massind = tspecies.getAttribute("mass");
minus_over_2m = -1./(2.*tspecies(massind,group_id));
return true;
}
where we may keep “group” and “minus_over_2m” as local variables to our specific class.
// In SpeciesKineticEnergy.h
private:
ParticleSet& tpset;
std::string group;
RealType minus_over_2m;
Notice that the previous operations are made possible by the saved reference to the target particle set. Last but not least, compile and run a full example (i.e., a short DMC calculation) with the following XML nodes in your input:
<estimator type="specieskinetic" name="ukinetic" group="u"/>
<estimator type="specieskinetic" name="dkinetic" group="d"/>
Make sure the sum of the “ukinetic” and “dkinetic” columns is exactly the same as the Kinetic columns at every block.
For easy reference, a summary of the complete list of changes follows:
// In HamiltonianFactory.cpp
#include "QMCHamiltonians/SpeciesKineticEnergy.h"
else if(potType =="specieskinetic")
{
SpeciesKineticEnergy* apot = new SpeciesKineticEnergy(*targetPtcl);
apot->put(cur);
targetH->addOperator(apot,potName,false);
}
// In SpeciesKineticEnergy.h
#include <Particle/WalkerSetRef.h>
#include <QMCHamiltonians/OperatorBase.h>
namespace qmcplusplus
{
class SpeciesKineticEnergy: public OperatorBase
{
public:
SpeciesKineticEnergy(ParticleSet& P):tpset(P){ };
// xml node is read by HamiltonianFactory, eg. the sum of following should be equivalent to Kinetic
// <estimator name="ukinetic" type="specieskinetic" target="e" group="u"/>
// <estimator name="dkinetic" type="specieskinetic" target="e" group="d"/>
bool put(xmlNodePtr cur); // read input xml node, required
bool get(std::ostream& os) const; // class description, required
Return_t evaluate(ParticleSet& P);
inline Return_t evaluate(ParticleSet& P, std::vector<NonLocalData>& Txy)
{ // delegate responsity inline for speed
return evaluate(P);
}
// pure virtual functions require overrider
void resetTargetParticleSet(ParticleSet& P) { } // required
OperatorBase* makeClone(ParticleSet& qp, TrialWaveFunction& psi); // required
private:
ParticleSet& tpset; // reference to target particle set
std::string group; // name of species to track
RealType minus_over_2m; // mass of the species !! assume same mass
// for multiple species, simply initialize multiple estimators
}; // SpeciesKineticEnergy
} // namespace qmcplusplus
#endif
// In SpeciesKineticEnergy.cpp
#include <QMCHamiltonians/SpeciesKineticEnergy.h>
#include <QMCHamiltonians/BareKineticEnergy.h> // laplaician() defined here
#include <OhmmsData/AttributeSet.h>
namespace qmcplusplus
{
bool SpeciesKineticEnergy::put(xmlNodePtr cur)
{
// read in extra parameter "group"
OhmmsAttributeSet attrib;
attrib.add(group,"group");
attrib.put(cur);
// save mass of specified group of particles
int group_id = tspecies.findSpecies(group);
int massind = tspecies.getAttribute("mass");
minus_over_2m = -1./(2.*tspecies(massind,group_id));
return true;
}
bool SpeciesKineticEnergy::get(std::ostream& os) const
{ // class description
os << "SpeciesKineticEnergy: " << myName << " for species " << group;
return true;
}
SpeciesKineticEnergy::Return_t SpeciesKineticEnergy::evaluate(ParticleSet& P)
{
Value = 0.0;
for (int iat=0; iat<P.getTotalNum(); iat++)
{
if (tspecies.speciesName[ P.GroupID(iat) ] == group)
{
Value += minus_over_2m*laplacian(P.G[iat],P.L[iat]);
}
}
return Value;
}
OperatorBase* SpeciesKineticEnergy::makeClone(ParticleSet& qp, TrialWaveFunction& psi)
{ //default constructor
return new SpeciesKineticEnergy(*this);
}
} // namespace qmcplusplus
Multiple scalars
It is fairly straightforward to create more than one column in the scalar.dat file with a single observable class. For example, if we want a single SpeciesKineticEnergy estimator to simultaneously record the kinetic energies of all species in the target particle set, we only have to write two new methods: addObservables() and setObservables(), then tweak the behavior of evaluate(). First, we will have to override the default behavior of addObservables() to make room for more than one column in the scalar.dat file as follows,
// In SpeciesKineticEnergy.cpp
void SpeciesKineticEnergy::addObservables(PropertySetType& plist, BufferType& collectables)
{
myIndex = plist.size();
for (int ispec=0; ispec<num_species; ispec++)
{ // make columns named "$myName_u", "$myName_d" etc.
plist.add(myName + "_" + species_names[ispec]);
}
}
where “num_species” and “species_name” can be local variables initialized in the constructor. We should also initialize some local arrays to hold temporary data.
// In SpeciesKineticEnergy.h
private:
int num_species;
std::vector<std::string> species_names;
std::vector<RealType> species_kinetic,vec_minus_over_2m;
// In SpeciesKineticEnergy.cpp
SpeciesKineticEnergy::SpeciesKineticEnergy(ParticleSet& P):tpset(P)
{
SpeciesSet& tspecies(P.getSpeciesSet());
int massind = tspecies.getAttribute("mass");
num_species = tspecies.size();
species_kinetic.resize(num_species);
vec_minus_over_2m.resize(num_species);
species_names.resize(num_species);
for (int ispec=0; ispec<num_species; ispec++)
{
species_names[ispec] = tspecies.speciesName[ispec];
vec_minus_over_2m[ispec] = -1./(2.*tspecies(massind,ispec));
}
}
Next, we need to override the default behavior of setObservables() to transfer multiple values to the property list kept by the main particle set, which eventually goes into the scalar.dat file.
// In SpeciesKineticEnergy.cpp
void SpeciesKineticEnergy::setObservables(PropertySetType& plist)
{ // slots in plist must be allocated by addObservables() first
copy(species_kinetic.begin(),species_kinetic.end(),plist.begin()+myIndex);
}
Finally, we need to change the behavior of evaluate() to fill the local vector “species_kinetic” with appropriate observable values.
SpeciesKineticEnergy::Return_t SpeciesKineticEnergy::evaluate(ParticleSet& P)
{
std::fill(species_kinetic.begin(),species_kinetic.end(),0.0);
for (int iat=0; iat<P.getTotalNum(); iat++)
{
int ispec = P.GroupID(iat);
species_kinetic[ispec] += vec_minus_over_2m[ispec]*laplacian(P.G[iat],P.L[iat]);
}
Value = 0.0; // Value is no longer used
return Value;
}
That’s it! The SpeciesKineticEnergy estimator no longer needs the “group” input and will automatically output the kinetic energy of every species in the target particle set in multiple columns. You should now be able to run with
<estimator type="specieskinetic" name="skinetic"/> and check that the sum of all columns that start with “skinetic” is equal to the default “Kinetic” column.
HDF5 output
If we desire an observable that will output hundreds of scalars per simulation step (e.g., SkEstimator), then it is preferred to output to the stat.h5 file instead of the scalar.dat file for better organization. A large chunk of data to be registered in the stat.h5 file is called a “Collectable” in QMCPACK. In particular, if a OperatorBase object is initialized with UpdateMode.set(COLLECTABLE,1), then the “Collectables” object carried by the main particle set will be processed and written to the stat.h5 file, where “UpdateMode” is a bit set (i.e., a collection of flags) with the following enumeration:
// In OperatorBase.h
///enum for UpdateMode
enum {PRIMARY=0,
OPTIMIZABLE=1,
RATIOUPDATE=2,
PHYSICAL=3,
COLLECTABLE=4,
NONLOCAL=5,
VIRTUALMOVES=6
};
As a simple example, to put the two columns we produced in the previous section into the stat.h5 file, we will first need to declare that our observable uses “Collectables.”
// In constructor add:
hdf5_out = true;
UpdateMode.set(COLLECTABLE,1);
Then make some room in the “Collectables” object carried by the target particle set.
// In addObservables(PropertySetType& plist, BufferType& collectables) add:
if (hdf5_out)
{
h5_index = collectables.size();
std::vector<RealType> tmp(num_species);
collectables.add(tmp.begin(),tmp.end());
}
Next, make some room in the stat.h5 file by overriding the registerCollectables() method.
// In SpeciesKineticEnergy.cpp
void SpeciesKineticEnergy::registerCollectables(std::vector<observable_helper>& h5desc, hid_t gid) const
{
if (hdf5_out)
{
std::vector<int> ndim(1,num_species);
observable_helper h5o(myName);
h5o.set_dimensions(ndim,h5_index);
h5o.open(gid);
h5desc.push_back(h5o);
}
}
Finally, edit evaluate() to use the space in the “Collectables” object.
// In SpeciesKineticEnergy.cpp
SpeciesKineticEnergy::Return_t SpeciesKineticEnergy::evaluate(ParticleSet& P)
{
RealType wgt = tWalker->Weight; // MUST explicitly use DMC weights in Collectables!
std::fill(species_kinetic.begin(),species_kinetic.end(),0.0);
for (int iat=0; iat<P.getTotalNum(); iat++)
{
int ispec = P.GroupID(iat);
species_kinetic[ispec] += vec_minus_over_2m[ispec]*laplacian(P.G[iat],P.L[iat]);
P.Collectables[h5_index + ispec] += vec_minus_over_2m[ispec]*laplacian(P.G[iat],P.L[iat])*wgt;
}
Value = 0.0; // Value is no longer used
return Value;
}
There should now be a new entry in the stat.h5 file containing the same columns of data as the stat.h5 file. After this check, we should clean up the code by
making “hdf5_out” and input flag by editing the put() method and
disabling output to
scalar.datwhen the “hdf5_out” flag is on.
Estimator output
Estimator definition
For simplicity, consider a local property \(O(\bf{R})\), where \(\bf{R}\) is the collection of all particle coordinates. An estimator for \(O(\bf{R})\) is a weighted average over walkers:
\(N^{tot}_{walker}\) is the total number of walkers collected in the entire simulation. Notice that \(N^{tot}_{walker}\) is typically far larger than the number of walkers held in memory at any given simulation step. \(w_i\) is the weight of walker \(i\).
In a VMC simulation, the weight of every walker is 1.0. Further, the number of walkers is constant at each step. Therefore, (276) simplifies to
Each walker \(\bf{R}_{s,e}\) is labeled by step index s and ensemble index e.
In a DMC simulation, the weight of each walker is different and may change from step to step. Further, the ensemble size varies from step to step. Therefore, (276) simplifies to
We will refer to the average in the \(\{\}\) as ensemble average and to the remaining averages as block average. The process of calculating \(O(\mathbf{R})\) is evaluate.
Class relations
A large number of classes are involved in the estimator collection process. They often have misleading class or method names. Check out the document gotchas in the following list:
EstimatorManageris an unused copy ofEstimatorManagerBase.EstimatorManagerBaseis the class used in the QMC drivers. (PR #371 explains this.)EstimatorManagerBase::Estimatorsis completely different fromQMCDriver::Estimators, which is subtly different fromOperatorBase::Estimators. The first is a list of pointers toScalarEstimatorBase. The second is the master estimator (one per MPI group). The third is the slave estimator that exists one per OpenMP thread.QMCHamiltonianis NOT a parent class ofOperatorBase. Instead,QMCHamiltonianowns two lists ofOperatorBasenamedHandauxH.QMCDriver::His NOT the same asQMCHamiltonian::H. The first is a pointer to aQMCHamiltonian.QMCHamiltonian::His a list.EstimatorManager::stopBlock(std::vector)is completely different fromEstimatorManager::stopBlock(RealType), which is the same asstopBlock(RealType, true)but that is subtly different fromstopBlock(RealType, false). The first three methods are intended to be called by the master estimator, which exists one per MPI group. The last method is intended to be called by the slave estimator, which exists one per OpenMP thread.
Estimator output stages
Estimators take four conceptual stages to propagate to the output files: evaluate, load ensemble, unload ensemble, and collect. They are easier to understand in reverse order.
Collect stage
File output is performed by the master EstimatorManager owned by QMCDriver. The first 8+ entries in EstimatorManagerBase::AverageCache will be written to scalar.dat. The remaining entries in AverageCache will be written to stat.h5. File writing is triggered by EstimatorManagerBase ::collectBlockAverages inside EstimatorManagerBase::stopBlock.
// In EstimatorManagerBase.cpp::collectBlockAverages
if(Archive)
{
*Archive << std::setw(10) << RecordCount;
int maxobjs=std::min(BlockAverages.size(),max4ascii);
for(int j=0; j<maxobjs; j++)
*Archive << std::setw(FieldWidth) << AverageCache[j];
for(int j=0; j<PropertyCache.size(); j++)
*Archive << std::setw(FieldWidth) << PropertyCache[j];
*Archive << std::endl;
for(int o=0; o<h5desc.size(); ++o)
h5desc[o]->write(AverageCache.data(),SquaredAverageCache.data());
H5Fflush(h_file,H5F_SCOPE_LOCAL);
}
EstimatorManagerBase::collectBlockAverages is triggered from the master-thread estimator via either stopBlock(std::vector) or stopBlock(RealType, true). Notice that file writing is NOT triggered by the slave-thread estimator method stopBlock(RealType, false).
// In EstimatorManagerBase.cpp
void EstimatorManagerBase::stopBlock(RealType accept, bool collectall)
{
//take block averages and update properties per block
PropertyCache[weightInd]=BlockWeight;
PropertyCache[cpuInd] = MyTimer.elapsed();
PropertyCache[acceptInd] = accept;
for(int i=0; i<Estimators.size(); i++)
Estimators[i]->takeBlockAverage(AverageCache.begin(),SquaredAverageCache.begin());
if(Collectables)
{
Collectables->takeBlockAverage(AverageCache.begin(),SquaredAverageCache.begin());
}
if(collectall)
collectBlockAverages(1);
}
// In ScalarEstimatorBase.h
template<typename IT>
inline void takeBlockAverage(IT first, IT first_sq)
{
first += FirstIndex;
first_sq += FirstIndex;
for(int i=0; i<scalars.size(); i++)
{
*first++ = scalars[i].mean();
*first_sq++ = scalars[i].mean2();
scalars_saved[i]=scalars[i]; //save current block
scalars[i].clear();
}
}
At the collect stage, calarEstimatorBase::scalars must be populated with ensemble-averaged data. Two derived classes of ScalarEstimatorBase are crucial: LocalEnergyEstimator will carry Properties, where as CollectablesEstimator will carry Collectables.
Unload ensemble stage
LocalEnergyEstimator::scalars are populated by
ScalarEstimatorBase::accumulate, whereas
CollectablesEstimator::scalars are populated by
CollectablesEstimator:: accumulate_all. Both accumulate methods
are triggered by EstimatorManagerBase::accumulate. One confusing
aspect about the unload stage is that
EstimatorManagerBase::accumulate has a master and a slave call
signature. A slave estimator such as QMCUpdateBase::Estimators
should unload a subset of walkers. Thus, the slave estimator should call
accumulate(W,it,it_end). However, the master estimator, such as
SimpleFixedNodeBranch::myEstimator, should unload data from the
entire walker ensemble. This is achieved by calling accumulate(W).
void EstimatorManagerBase::accumulate(MCWalkerConfiguration& W)
{ // intended to be called by master estimator only
BlockWeight += W.getActiveWalkers();
RealType norm=1.0/W.getGlobalNumWalkers();
for(int i=0; i< Estimators.size(); i++)
Estimators[i]->accumulate(W,W.begin(),W.end(),norm);
if(Collectables)//collectables are normalized by QMC drivers
Collectables->accumulate_all(W.Collectables,1.0);
}
void EstimatorManagerBase::accumulate(MCWalkerConfiguration& W
, MCWalkerConfiguration::iterator it
, MCWalkerConfiguration::iterator it_end)
{ // intended to be called slaveEstimator only
BlockWeight += it_end-it;
RealType norm=1.0/W.getGlobalNumWalkers();
for(int i=0; i< Estimators.size(); i++)
Estimators[i]->accumulate(W,it,it_end,norm);
if(Collectables)
Collectables->accumulate_all(W.Collectables,1.0);
}
// In LocalEnergyEstimator.h
inline void accumulate(const Walker_t& awalker, RealType wgt)
{ // ensemble average W.Properties
// expect ePtr to be W.Properties; expect wgt = 1/GlobalNumberOfWalkers
const RealType* restrict ePtr = awalker.getPropertyBase();
RealType wwght= wgt* awalker.Weight;
scalars[0](ePtr[WP::LOCALENERGY],wwght);
scalars[1](ePtr[WP::LOCALENERGY]*ePtr[WP::LOCALENERGY],wwght);
scalars[2](ePtr[LOCALPOTENTIAL],wwght);
for(int target=3, source=FirstHamiltonian; target<scalars.size(); ++target, ++source)
scalars[target](ePtr[source],wwght);
}
// In CollectablesEstimator.h
inline void accumulate_all(const MCWalkerConfiguration::Buffer_t& data, RealType wgt)
{ // ensemble average W.Collectables
// expect data to be W.Collectables; expect wgt = 1.0
for(int i=0; i<data.size(); ++i)
scalars[i](data[i], wgt);
}
At the unload ensemble stage, the data structures Properties and Collectables must be populated by appropriately normalized values so that the ensemble average can be correctly taken. QMCDriver is responsible for the correct loading of data onto the walker ensemble.
Load ensemble stage
Properties in the MC ensemble of walkers QMCDriver::W is
populated by QMCHamiltonian::saveProperties. The master QMCHamiltonian::LocalEnergy,
::KineticEnergy, and ::Observables must be properly populated
at the end of the evaluate stage.// In QMCHamiltonian.h
template<class IT>
inline
void saveProperty(IT first)
{ // expect first to be W.Properties
first[LOCALPOTENTIAL]= LocalEnergy-KineticEnergy;
copy(Observables.begin(),Observables.end(),first+myIndex);
}
Collectables’s load stage is combined with its evaluate stage.
Evaluate stage
QMCHamiltonian::Observables is populated by slave
OperatorBase ::setObservables. However, the call signature
must be OperatorBase::setObservables (QMCHamiltonian::Observables). This call signature is enforced by
QMCHamiltonian::evaluate and QMCHamiltonian::auxHevaluate.// In QMCHamiltonian.cpp
QMCHamiltonian::Return_t
QMCHamiltonian::evaluate(ParticleSet& P)
{
LocalEnergy = 0.0;
for(int i=0; i<H.size(); ++i)
{
myTimers[i]->start();
LocalEnergy += H[i]->evaluate(P);
H[i]->setObservables(Observables);
#if !defined(REMOVE_TRACEMANAGER)
H[i]->collect_scalar_traces();
#endif
myTimers[i]->stop();
H[i]->setParticlePropertyList(P.PropertyList,myIndex);
}
KineticEnergy=H[0]->Value;
P.PropertyList[WP::LOCALENERGY]=LocalEnergy;
P.PropertyList[LOCALPOTENTIAL]=LocalEnergy-KineticEnergy;
// auxHevaluate(P);
return LocalEnergy;
}
// In QMCHamiltonian.cpp
void QMCHamiltonian::auxHevaluate(ParticleSet& P, Walker_t& ThisWalker)
{
#if !defined(REMOVE_TRACEMANAGER)
collect_walker_traces(ThisWalker,P.current_step);
#endif
for(int i=0; i<auxH.size(); ++i)
{
auxH[i]->setHistories(ThisWalker);
RealType sink = auxH[i]->evaluate(P);
auxH[i]->setObservables(Observables);
#if !defined(REMOVE_TRACEMANAGER)
auxH[i]->collect_scalar_traces();
#endif
auxH[i]->setParticlePropertyList(P.PropertyList,myIndex);
}
}
Estimator use cases
VMCSingleOMP pseudo code
bool VMCSingleOMP::run()
{
masterEstimator->start(nBlocks);
for (int ip=0; ip<NumThreads; ++ip)
Movers[ip]->startRun(nBlocks,false); // slaveEstimator->start(blocks, record)
do // block
{
#pragma omp parallel
{
Movers[ip]->startBlock(nSteps); // slaveEstimator->startBlock(steps)
RealType cnorm = 1.0/static_cast<RealType>(wPerNode[ip+1]-wPerNode[ip]);
do // step
{
wClones[ip]->resetCollectables();
Movers[ip]->advanceWalkers(wit, wit_end, recompute);
wClones[ip]->Collectables *= cnorm;
Movers[ip]->accumulate(wit, wit_end);
} // end step
Movers[ip]->stopBlock(false); // slaveEstimator->stopBlock(acc, false)
} // end omp
masterEstimator->stopBlock(estimatorClones); // write files
} // end block
masterEstimator->stop(estimatorClones);
}
DMCOMP pseudo code
bool DMCOMP::run()
{
masterEstimator->setCollectionMode(true);
masterEstimator->start(nBlocks);
for(int ip=0; ip<NumThreads; ip++)
Movers[ip]->startRun(nBlocks,false); // slaveEstimator->start(blocks, record)
do // block
{
masterEstimator->startBlock(nSteps);
for(int ip=0; ip<NumThreads; ip++)
Movers[ip]->startBlock(nSteps); // slaveEstimator->startBlock(steps)
do // step
{
#pragma omp parallel
{
wClones[ip]->resetCollectables();
// advanceWalkers
} // end omp
//branchEngine->branch
{ // In WalkerControlMPI.cpp::branch
wgt_inv=WalkerController->NumContexts/WalkerController->EnsembleProperty.Weight;
walkers.Collectables *= wgt_inv;
slaveEstimator->accumulate(walkers);
}
masterEstimator->stopBlock(acc) // write files
} // end for step
} // end for block
masterEstimator->stop();
}
Summary
Two ensemble-level data structures, ParticleSet::Properties and
::Collectables, serve as intermediaries between evaluate classes and
output classes to scalar.dat and stat.h5. Properties appears
in both scalar.dat and stat.h5, whereas Collectables appears
only in stat.h5. Properties is overwritten by
QMCHamiltonian::Observables at the end of each step.
QMCHamiltonian::Observables is filled upon call to
QMCHamiltonian::evaluate and ::auxHevaluate. Collectables is
zeroed at the beginning of each step and accumulated upon call to
::auxHevaluate.
scalar.dat in four stages: evaluate, load,
unload, and collect. In the evaluate stage,
QMCHamiltonian::Observables is populated by a list of
OperatorBase. In the load stage, QMCHamiltonian::Observables
is transferred to Properties by QMCDriver. In the unload stage,
Properties is copied to LocalEnergyEstimator::scalars. In the
collect stage, LocalEnergyEstimator::scalars is block-averaged to
EstimatorManagerBase::AverageCache and dumped to file. For Collectables, the
evaluate and load stages are combined in a call to
QMCHamiltonian::auxHevaluate. In the unload stage,
Collectables is copied to CollectablesEstimator::scalars. In
the collect stage, CollectablesEstimator::scalars is block-averaged to
EstimatorManagerBase::AverageCache and dumped to file.Appendix: dmc.dat
ParticleSet::EnsembleProperty, that is managed by
WalkerControlBase::EnsembleProperty and directly dumped to
dmc.dat via its own averaging procedure. dmc.dat is written by
WalkerControlBase::measureProperties, which is called by
WalkerControlBase::branch, which is called by
SimpleFixedNodeBranch::branch, for example.- KCM93(1,2,3)
Yongkyung Kwon, D. M. Ceperley, and Richard M. Martin. Effects of three-body and backflow correlations in the two-dimensional electron gas. Phys. Rev. B, 48:12037–12046, October 1993. doi:10.1103/PhysRevB.48.12037.
- TU07
Julien Toulouse and C. J. Umrigar. Optimization of quantum monte carlo wave functions by energy minimization. The Journal of Chemical Physics, 126(8):084102, 2007. arXiv:http://dx.doi.org/10.1063/1.2437215, doi:10.1063/1.2437215.
Comments
Comment style
Use the
// Commentsyntax for actual comments.Use
or
Documentation
Doxygen will be used for source documentation. Doxygen commands should be used when appropriate guidance on this has been decided.
File docs
Do not put the file name after the
\fileDoxygen command. Doxygen will fill it in for the file the tag appears in.Class docs
Every class should have a short description (in the header of the file) of what it is and what is does. Comments for public class member functions follow the same rules as general function comments. Comments for private members are allowed but are not mandatory.
Function docs
For function parameters whose type is non-const reference or pointer to non-const memory, it should be specified if they are input (In:), output (Out:) or input-output parameters (InOut:).
Example:
Variable documentation
Name should be self-descriptive. If you need documentation consider renaming first.
Golden rule of comments
If you modify a piece of code, also adapt the comments that belong to it if necessary.