QMCPACK Design and Feature Documentation
This section contains information on the overall design of QMCPACK. Also included are detailed explanations/derivations of major features and algorithms present in the code.
QMCPACK design
TBD.
Feature: Optimized long-range breakup (Ewald)
Consider a group of particles interacting with long-range central potentials, \(v^{\alpha \beta}(|r^{\alpha}_i - r^{\beta}_j|)\), where the Greek superscripts represent the particle species (e.g., \(\alpha=\text{electron}\), \(\beta=\text{proton}\)), and Roman subscripts refer to particle number within a species. We can then write the total interaction energy for the system as
The long-range problem
Consider such a system in periodic boundary conditions in a cell defined by primitive lattice vectors \(\mathbf{a}_1\), \(\mathbf{a}_2\), and \(\mathbf{a}_3\). Let \(\mathbf{L}\equiv n_1 \mathbf{a}_1 + n_2 \mathbf{a}_2 + n_3\mathbf{a}_3\) be a direct lattice vector. Then the interaction energy per cell for the periodic system is given by
where \(N^\alpha\) is the number particles of species \(\alpha\). If the potentials \(v^{\alpha\beta}(r)\) are indeed long-range, the summation over direct lattice vectors will not converge in this naive form. A solution to the problem was posited by Ewald. We break the central potentials into two pieces—a short-range and a long-range part defined by
We will perform the summation over images for the short-range part in real space, while performing the sum for the long-range part in reciprocal space. For simplicity, we choose \(v^{\alpha \beta}_s(r)\) so that it is identically zero at the half-the-box length. This eliminates the need to sum over images in real space.
Reciprocal-space sums
Heterologous terms
We begin with (94), starting with the heterologous terms (i.e., the terms involving particles of different species). The short-range terms are trivial, so we neglect them here.
We insert the resolution of unity in real space twice:
Here, the \(\mathbf{k}\) summations are over reciprocal lattice vectors given by \(\mathbf{k}= m_1 \mathbf{b}_1 + m_2\mathbf{b}_2 + m_3\mathbf{b}_3\), where
We note that \(\mathbf{k}\cdot \mathbf{L}= 2\pi(n_1 m_1 + n_2 m_2 + n_3 m_3)\).
where \(\Omega\) is the volume of the cell. Here we have used the fact that summing over all cells of the integral over the cell is equivalent to integrating over all space.
We have
Then, performing the integrations we have
We now separate the summations, yielding
Summing over \(\mathbf{k}\) and \(\mathbf{k}'\), we have
We can simplify the calculation a bit further by rearranging the sums over species:
Homologous terms
We now consider the terms involving particles of the same species interacting with each other. The algebra is very similar to the preceding, with the slight difficulty of avoiding the self-interaction term.
Madelung terms
Let us now consider the Madelung term for a single particle of species \(\alpha\). This term corresponds to the interaction of a particle with all of its periodic images.
\(\mathbf{k}=\mathbf{0}\) terms
Thus far, we have neglected what happens at the special point \(\mathbf{k}= \mathbf{0}\). For many long-range potentials, such as the Coulomb potential, \(v_k^{\alpha \alpha}\) diverges for \(k=0\). However, we recognize that for a charge-neutral system, the divergent part of the terms cancel each other. If all the potential in the system were precisely Coulomb, the \(\mathbf{k}=\mathbf{0}\) terms would cancel precisely, yielding zero. For systems involving PPs, however, it may be that the resulting term is finite, but nonzero. Consider the terms from \(\mathbf{k}=\mathbf{0}\):
Next, we must compute \(v^{\alpha \beta}_{k=0}\).
We recognize that this integral will not converge because of the large-\(r\) behavior. However, we recognize that when we do the sum in (109), the large-\(r\) parts of the integrals will cancel precisely. Therefore, we define
where \(r_{\text{end}}\) is some cutoff value after which the potential tails precisely cancel.
Neutralizing background terms
For systems with a net charge, such as the one-component plasma (jellium), we add a uniform background charge, which makes the system neutral. When we do this, we must add a term that comes from the interaction of the particle with the neutral background. It is a constant term, independent of the particle positions. In general, we have a compensating background for each species, which largely cancels out for neutral systems.
where \(v^{\alpha \beta}_{s\mathbf{0}}\) is given by
Combining terms
Here, we sum all of the terms we computed in the previous sections:
Computing the reciprocal potential
Now we return to (99). Without loss of generality, we define for convenience \(\mathbf{k}= k\hat{\mathbf{z}}\).
We do the angular integral first. By inversion symmetry, the imaginary part of the integral vanishes, yielding
The Coulomb potential
For the case of the Coulomb potential, the preceding integral is not formally convergent if we do the integral naively. We may remedy the situation by including a convergence factor, \(e^{-k_0 r}\). For a potential of the form \(v^{\text{coul}}(r) = q_1 q_2/r\), this yields
Allowing the convergence factor to tend to zero, we have
For more generalized potentials with a Coulomb tail, we cannot evaluate (116) numerically but must handle the coulomb part analytically. In this case, we have
Efficient calculation methods
Fast computation of \(\rho_\mathbf{k}\)
We wish to quickly calculate the quantity
First, we write
Now, we note that
This allows us to recursively build up an array of the \(C^{i\alpha}\)s and then compute \(\rho_\mathbf{k}\) for all \(\mathbf{k}\)-vectors by looping over all k-vectors, requiring only two complex multiplies per particle per \(\mathbf{k}\).
Algorithm to quickly calculate \(\rho_\mathbf{k}^\alpha\).
Gaussian charge screening breakup
This original approach to the short- and long-range breakup adds an opposite screening charge of Gaussian shape around each point charge. It then removes the charge in the long-range part of the potential. In this potential,
where \(\alpha\) is an adjustable parameter used to control how short ranged the potential should be. If the box size is \(L\), a typical value for \(\alpha\) might be \(7/(Lq_1 q_2)\). We should note that this form for the long-range potential should also work for any general potential with a Coulomb tail (e.g., pseudo-Hamiltonian potentials. For this form of the long-range potential, we have in \(k\)-space
Optimized breakup method
In this section, we undertake the task of choosing a long-range/short-range partitioning of the potential, which is optimal in that it minimizes the error for given real and \(k\)-space cutoffs \(r_c\) and \(k_c\). Here, we slightly modify the method introduced by Natoli and Ceperley [NC95]. We choose \(r_c = \frac{1}{2}\min\{L_i\}\) so that we require the nearest image in real-space summation. \(k_c\) is then chosen to satisfy our accuracy requirements.
Here we modify our notation slightly to accommodate details not previously required. We restrict our discussion to the interaction of two particle species (which may be the same), and drop our species indices. Thus, we are looking for short- and long-range potentials defined by
Define \(v^s_k\) and \(v^\ell_k\) to be the respective Fourier transforms of the previous equation. The goal is to choose \(v_s(r)\) such that its value and first two derivatives vanish at \(r_c\), while making \(v^\ell(r)\) as smooth as possible so that \(k\)-space components, \(v^\ell_k\), are very small for \(k>k_c\). Here, we describe how to do this in an optimal way.
Define the periodic potential, \(V_p\), as
where \(\mathbf{r}\) is the displacement between the two particles and \(\mathbf{l}\) is a lattice vector. Let us then define our approximation to this potential, \(V_a\), as
Now, we seek to minimize the RMS error over the cell,
We may write
where
We now need a basis in which to represent the broken-up potential. We may choose to represent either \(v^s(r)\) or \(v^\ell(r)\) in a real-space basis. Natoli and Ceperley chose the former in their paper. We choose the latter for a number of reasons. First, singular potentials are difficult to represent in a linear basis unless the singularity is explicitly included. This requires a separate basis for each type of singularity. The short-range potential may have an arbitrary number of features for \(r<r_c\) and still be a valid potential. By construction, however, we desire that \(v^\ell(r)\) be smooth in real-space so that its Fourier transform falls off quickly with increasing \(k\). We therefore expect that, in general, \(v^\ell(r)\) should be well represented by fewer basis functions than \(v^s(r)\). Therefore, we define
where the \(h_n(r)\) are a set of \(J\) basis functions. We require that the two cases agree on the value and first two derivatives at \(r_c\). We may then define
Similarly, we define
Therefore,
Because \(v^s(r)\) goes identically to zero at the box edge, inside the cell we may write
We then write
We see that if we define
Then
which then cancels out all terms for \(|\mathbf{k}| < k_c\). Then we have
We expand the summation,
We take the derivative w.r.t. \(t_{m}\):
We integrate w.r.t. \(\mathbf{r}\), yielding a Kronecker \(\delta\).
Summing over \(\mathbf{k}'\) and equating the derivative to zero, we find the minimum of our error function is given by
which is equivalent in form to Equation 19 in [NC95], where we have \(x_k\) instead of \(V_k\). Thus, we see that we can optimize the short- or long-range potential simply by choosing to use \(V_k\) or \(x_k\) in the preceding equation. We now define
Thus, it becomes clear that our minimization equations can be cast in the canonical linear form
Solution by SVD
In practice, we note that the matrix \(\mathbf{A}\) frequently becomes singular in practice. For this reason, we use the singular value decomposition to solve for \(t_n\). This factorization decomposes \(A\) as
where \(\mathbf{U}^T\mathbf{U}= \mathbf{V}^T\mathbf{V}= 1\) and \(\mathbf{S}\) is diagonal. In this form, we have
where the parenthesized subscripts refer to columns. The advantage of this form is that if \(\mathbf{S}_{ii}\) is zero or very near zero, the contribution of the \(i^{\text{th}}\) of \(\mathbf{V}\) may be neglected since it represents a numerical instability and has little physical meaning. It represents the fact that the system cannot distinguish between two linear combinations of the basis functions. Using the SVD in this manner is guaranteed to be stable. This decomposition is available in LAPACK in the DGESVD subroutine.
Constraining Values
Often, we wish to constrain the value of \(t_n\) to have a fixed value to enforce a boundary condition, for example. To do this, we define
We then define \(\mathbf{A}^*\) as \(\mathbf{A}\) with the \(n^{\text{th}}\) row and column removed and \(\mathbf{b}^*\) as \(\mathbf{b}'\) with the \(n^{\text{th}}\) element removed. Then we solve the reduced equation \(\mathbf{A}^* \mathbf{t}^* = \mathbf{b}^*\) and finally insert \(t_n\) back into the appropriate place in \(\mathbf{t}^*\) to recover the complete, constrained vector \(\mathbf{t}\). This may be trivially generalized to an arbitrary number of constraints.
The LPQHI basis
The preceding discussion is general and independent of the basis used to represent \(v^\ell(r)\). In this section, we introduce a convenient basis of localized interpolant functions, similar to those used for splines, which have a number of properties that are convenient for our purposes.
First, we divide the region from 0 to \(r_c\) into \(M-1\) subregions, bounded above and below by points we term knots, defined by \(r_j \equiv j\Delta\), where \(\Delta \equiv r_c/(M-1)\). We then define compact basis elements, \(h_{j\alpha}\), which span the region \([r_{j-1},r_{j+1}]\), except for \(j=0\) and \(j=M\). For \(j=0\), only the region \([r_0,r_1]\), while for \(j=M\), only \([r_{M-1}, r_M]\). Thus, the index \(j\) identifies the knot the element is centered on, while \(\alpha\) is an integer from 0 to 2 indicating one of three function shapes. The dual index can be mapped to the preceding single index by the relation \(n = 3j + \alpha\). The basis functions are then defined as
where the matrix \(S_{\alpha n}\) is given by
Fig. 28 shows plots of these function shapes.
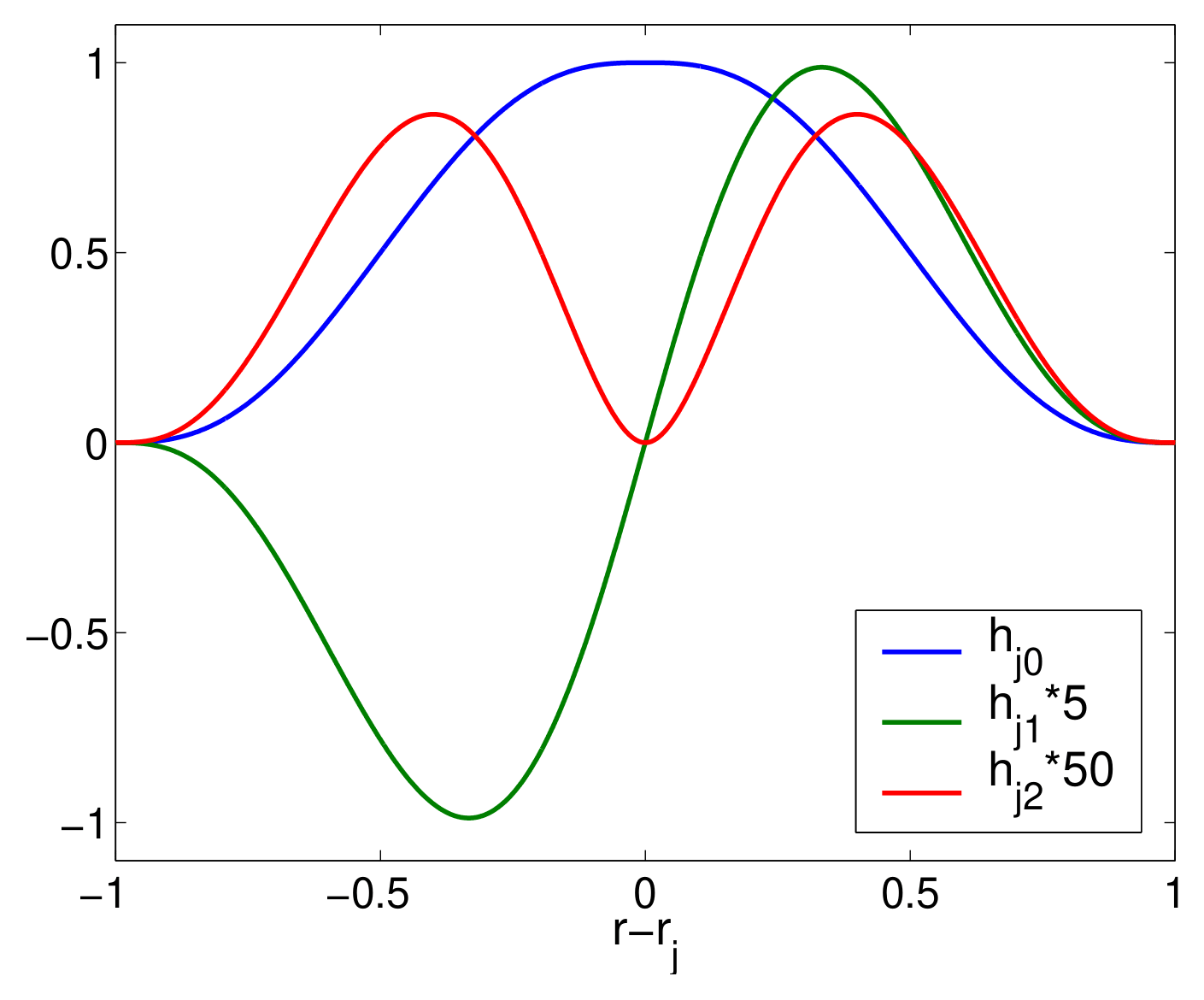
Fig. 28 Basis functions \(h_{j0}\), \(h_{j1}\), and \(h_{j2}\) are shown. We note that at the left and right extremes, the values and first two derivatives of the functions are zero; while at the center, \(h_{j0}\) has a value of 1, \(h_{j1}\) has a first derivative of 1, and \(h_{j2}\) has a second derivative of 1.
The basis functions have the property that at the left and right extremes (i.e., \(r_{j-1}\) and \(r_{j+1}\)) their values and first two derivatives are zero. At the center, \(r_j\), we have the properties
These properties allow the control of the value and first two derivatives of the represented function at any knot value simply by setting the coefficients of the basis functions centered around that knot. Used in combination with the method described in Constraining Values, boundary conditions can easily be enforced. In our case, we wish require that
This ensures that \(v^s\) and its first two derivatives vanish at \(r_c\).
Fourier coefficients
We wish now to calculate the Fourier transforms of the basis functions, defined as
We may then write,
where
We then further make the definition that
It can then be shown that
Note that these equations correct typographical errors present in [NC95].
Enumerating \(k\)-points
We note that the summations over \(k\), which are ubiquitous in this paper, require enumeration of the \(k\)-vectors. In particular, we should sum over all \(|\mathbf{k}| > k_c\). In practice, we must limit our summation to some finite cutoff value \(k_c < |\mathbf{k}| < k_{\text{max}}\), where \(k_{\text{max}}\) should be on the order of \(3,000/L\), where \(L\) is the minimum box dimension. Enumerating these vectors in a naive fashion even for this finite cutoff would prove quite prohibitive, as it would require \(\sim10^9\) vectors.
Our first optimization comes in realizing that all quantities in this calculation require only \(|\mathbf{k}|\) and not \(\mathbf{k}\) itself. Thus, we may take advantage of the great degeneracy of \(|\mathbf{k}|\). We create a list of \((k,N)\) pairs, where \(N\) is the number of vectors with magnitude \(k\). We make nested loops over \(n_1\), \(n_2\), and \(n_3\), yielding \(\mathbf{k}= n_1 \mathbf{b}_1 + n_2 \mathbf{b}_2 + n_3 \mathbf{b}_3\). If \(|\mathbf{k}|\) is in the required range, we check to see whether there is already an entry with that magnitude on our list and increment the corresponding \(N\) if there is, or create a new entry if not. Doing so typically saves a factor of \(\sim200\) in storage and computation.
This reduction is not sufficient for large \(k_max\) since it requires that we still look over \(10^9\) entries. To further reduce costs, we may pick an intermediate cutoff, \(k_{\text{cont}}\), above which we will approximate the degeneracy assuming a continuum of \(k\)-points. We stop our exact enumeration at \(k_{\text{cont}}\) and then add \(\sim1,000\) points, \(k_i\), uniformly spaced between \(k_{\text{cont}}\) and \(k_{\text{max}}\). We then approximate the degeneracy by
where \(k_b = (k_i + k_{i+1})/2\) and \(k_a = (k_i + k_{i-1})\). In doing so, we typically reduce our total number of k-points to sum more than \(\sim2,500\) from the \(10^9\) we had to start.
Calculating \(x_k\)’s
The Coulomb potential
For \(v(r) = \frac{1}{r}\), \(x_k\) is given by
The \(1/r^2\) potential
For \(v(r) = \frac{1}{r^2}\), \(x_k\) is given by
where the sin integral, \(\text{Si}(z)\), is given by
The \(1/r^3\) potential
For \(v(r) = \frac{1}{r^3}\), \(x_k\) is given by
where the cosine integral, \(\text{Ci}(z)\), is given by
The \(1/r^4\) potential
For \(v(r) = \frac{1}{r^4}\), \(x_k\) is given by
Feature: Optimized long-range breakup (Ewald) 2
Given a lattice of vectors \(\mathbf{L}\), its associated reciprocal lattice of vectors \(\mathbf{k}\) and a function \(\psi(\mathbf{r})\) periodic on the lattice we define its Fourier transform \(\widetilde{\psi}(\mathbf{k})\) as
where we indicated both the cell domain and the cell volume by \(\Omega\). \(\psi(\mathbf{r})\) can then be expressed as
The potential generated by charges sitting on the lattice positions at a particular point \(\mathbf{r}\) inside the cell is given by
and its Fourier transform can be explicitly written as a function of \(V\) or \(v\)
where \(\mathbb{R}^3\) denotes the whole 3D space. We now want to find the best (“best” to be defined later) approximate potential of the form
where \(W(r)\) has been chosen to go smoothly to \(0\) when \(r=r_c\), being \(r_c\) lower or equal to the Wigner-Seitz radius of the cell. Note also the cutoff \(k_c\) on the momentum summation.
The best form of \(\widetilde{Y}(k)\) and \(W(r)\) is given by minimizing
or the reciprocal space equivalent
(171) follows from (170) and the unitarity (norm conservation) of the Fourier transform.
This last condition is minimized by
We now use a set of basis function \(c_i(r)\) vanishing smoothly at \(r_c\) to expand \(W(r)\); that is,
Inserting the reciprocal space expansion of \(\widetilde{W}\) in the second condition of (172) and minimizing with respect to \(t_i\) leads immediately to the linear system \(\mathbf{A}\mathbf{t}=\mathbf{b}\) where
Basis functions
The basis functions are splines. We define a uniform grid with \(N_{\text{knot}}\) uniformly spaced knots at position \(r_i=i\frac{r_c}{N_{\text{knot}}}\), where \(i\in[0,N_{\text{knot}}-1]\). On each knot we center \(m+1\) piecewise polynomials \(c_{i\alpha}(r)\) with \(\alpha\in[0,m]\), defined as
These functions and their derivatives are, by construction, continuous and odd (even) (with respect to \(r-r_i\rightarrow r_i-r\)) when \(\alpha\) is odd (even). We further ask them to satisfy
(The parity of the functions guarantees that the second constraint is satisfied at \(r_{i-1}\) as well). These constraints have a simple interpretation: the basis functions and their first \(m\) derivatives are \(0\) on the boundary of the subinterval where they are defined; the only function to have a nonzero \(\beta\)-th derivative in \(r_i\) is \(c_{i\beta}\). These \(2(m+1)\) constraints therefore impose \(\mathcal{N}=2m+1\). Inserting the definitions of (175) in the constraints of (176) leads to the set of \(2(m+1)\) linear equation that fixes the value of \(S_{\alpha n}\):
We can further simplify inserting the first of these equations into the second and write the linear system as
Fourier components of the basis functions in 3D
\(k\ne 0\), non-Coulomb case
We now need to evaluate the Fourier transform \(\widetilde{c}_{i\alpha}(k)\). Let us start by writing the definition
Because \(c_{i\alpha}\) is different from zero only inside the spherical crown defined by \(r_{i-1}<r<r_i\), we can conveniently compute the integral in spherical coordinates as
where we used the definition \(w_{\text{knot}}=1-\delta_{i0}\) and
obtained by integrating the angular part of the Fourier transform. Using the identity
and the definition
we rewrite Equation (181) as
Finally, using integration by part, we can define \(E^\pm_{in}\) recursively as
Starting from the \(n=0\) term,
\(k\ne 0\), Coulomb case
To efficiently treat the Coulomb divergence at the origin, it is convenient to use a basis set \(c_{i\alpha}^{\text{coul}}\) of the form
An equation identical to (181) holds but with the modified definition
which can be simply expressed using \(E^\pm_{in}(k)\) as
\(k=0\) Coulomb and non-Coulomb case
The definitions of \(D_{in}(k)\) given so far are clearly incompatible with the choice \(k=0\) (they involve division by \(k\)). For the non-Coulomb case, the starting definition is
Using the definition \(I_n^\pm=(\pm)^{n+1}\Delta/(n+1)\), we can express this as
For the Coulomb case, we get
Fourier components of the basis functions in 2D
(180) still holds provided we define
where \(C=1(=0)\) for the Coulomb(non-Coulomb) case. (192) is obtained using the integral definition of the zero order Bessel function of the first kind:
and the binomial expansion for \((r-r_i)^n\). The integrals can be computed recursively using the following identities:
The bottom equation of (194) is obtained using the second equation in the same set, integration by part, and the identity \(\int J_1(z) dz =-J_0(z)\). In the top equation, \(H_0\) and \(H_1\) are Struve functions.
Construction of the matrix elements
Using the previous equations, we can construct the matrix elements in (174) and proceed solving for \(t_i\). It is sometimes desirable to put some constraints on the value of \(t_i\). For example, when the Coulomb potential is concerned, we might want to set \(t_{0}=1\). If the first \(g\) variable is constrained by \(t_{m}=\gamma_m\) with \(m=[1,g]\), we can simply redefine (174) as
Feature: Cubic spline interpolation
We present the basic equations and algorithms necessary to construct and evaluate cubic interpolating splines in one, two, and three dimensions. Equations are provided for both natural and periodic boundary conditions.
One dimension
Let us consider the problem in which we have a function \(y(x)\) specified at a discrete set of points \(x_i\), such that \(y(x_i) = y_i\). We wish to construct a piecewise cubic polynomial interpolating function, \(f(x)\), which satisfies the following conditions:
\(f(x_i) = y_i\).
\(f'(x_i^-) = f'(x_i^+)\).
\(f''(x_i^-) = f''(x_i+)\).
Hermite interpolants
In our piecewise representation, we wish to store only the values \(y_i\) and first derivatives, \(y'_i\), of our function at each point \(x_i\), which we call knots. Given this data, we wish to construct the piecewise cubic function to use between \(x_i\) and \(x_{i+1}\), which satisfies the preceding conditions. In particular, we wish to find the unique cubic polynomial, \(P(x)\), satisfying
We then define the basis functions,
On the interval, \((x_i, x_{i+1}]\), we define the interpolating function
It can be easily verified that \(P(x)\) satisfies conditions of equations 1 through 3 of (196). It is now left to determine the proper values for the \(y'_i\,\)s such that the continuity conditions given previously are satisfied.
By construction, the value of the function and derivative will match at the knots; that is,
Then we must now enforce only the second derivative continuity:
Let us define
Then we may rearrange
This equation holds for all \(0<i<(N-1)\), so we have a tridiagonal set of equations. The equations for \(i=0\) and \(i=N-1\) depend on the boundary conditions we are using.
Periodic boundary conditions
For periodic boundary conditions, we have
Or, in matrix form, we have
The system is tridiagonal except for the two elements in the upper right and lower left corners. These terms complicate the solution a bit, although it can still be done in \(\mathcal{O}(N)\) time. We first proceed down the rows, eliminating the the first non-zero term in each row by subtracting the appropriate multiple of the previous row. At the same time, we eliminate the first element in the last row, shifting the position of the first non-zero element to the right with each iteration. When we get to the final row, we will have the value for \(y'_{N-1}\). We can then proceed back upward, backsubstituting values from the rows below to calculate all the derivatives.
Complete boundary conditions
If we specify the first derivatives of our function at the end points, we have what is known as complete boundary conditions. The equations in that case are trivial to solve:
This system is completely tridiagonal, and we may solve trivially by performing row eliminations downward, then proceeding upward as before.
Natural boundary conditions
If we do not have information about the derivatives at the boundary conditions, we may construct a natural spline, which assumes the second derivatives are zero at the end points of our spline. In this case our system of equations is the following:
with
Bicubic splines
It is possible to extend the cubic spline interpolation method to functions of two variables, that is, \(F(x,y)\). In this case, we have a rectangular mesh of points given by \(F_{ij} \equiv F(x_i,y_j)\). In the case of 1D splines, we needed to store the value of the first derivative of the function at each point, in addition to the value. In the case of bicubic splines, we need to store four quantities for each mesh point:
Consider the point \((x,y)\) at which we wish to interpolate \(F\). We locate the rectangle that contains this point, such that \(x_i <= x < x_{i+1}\) and \(y_i <= x < y_{i+1}\). Let
Then, we calculate the interpolated value as
Construction bicubic splines
We now address the issue of how to compute the derivatives that are needed for the interpolation. The algorithm is quite simple. For every \(x_i\), we perform the tridiagonal solution as we did in the 1D splines to compute \(F^y_{ij}\). Similarly, we perform a tridiagonal solve for every value of \(F^x_{ij}\). Finally, to compute the cross-derivative we may either to the tridiagonal solve in the \(y\) direction of \(F^x_{ij}\), or solve in the \(x\) direction for \(F^y_{ij}\) to obtain the cross-derivatives \(F^{xy}_{ij}\). Hence, only minor modifications to the \(1D\) interpolations are necessary.
Tricubic splines
Bicubic interpolation required two 4-component vectors and a \(4 \times 4\) matrix. By extension, tricubic interpolation requires three 4-component vectors and a \(4 \times 4 \times 4\) tensor. We summarize the forms of these vectors in the following:
Now, we can write
The appropriate derivatives of \(F\) may be computed by a generalization of the previous method used for bicubic splines.
Feature: B-spline orbital tiling (band unfolding)
In continuum QMC simulations, it is necessary to evaluate the electronic orbitals of a system at real-space positions hundreds of millions of times. It has been found that if these orbitals are represented in a localized, B-spline basis, each evaluation takes a small, constant time that is independent of system size.
Unfortunately, the memory required for storing the B-spline grows with the second power of the system size. If we are studying perfect crystals, however, this can be reduced to linear scaling if we tile the primitive cell. In this approach, a supercell is constructed by tiling the primitive cell \(N_1 \times N_2 \times N_3\) in the three lattice directions. The orbitals are then represented in real space only in the primitive cell and an \(N_1 \times N_2 \times N_3\) k-point mesh. To evaluate an orbital at any point in the supercell, it is only necessary to wrap that point back into the primitive cell, evaluate the spline, and then multiply the phase factor, \(e^{-i\mathbf{k}\cdot\mathbf{r}}\).
Here, we show that this approach can be generalized to a tiling constructed with a \(3\times 3\) nonsingular matrix of integers, of which the preceding approach is a special case. This generalization brings with it a number of advantages. The primary reason for performing supercell calculations in QMC is to reduce finite-size errors. These errors result from three sources: (1) the quantization of the crystal momentum, (2) the unphysical periodicity of the exchange-correlation (XC) hole of the electron, and (3) the kinetic-energy contribution from the periodicity of the long-range Jastrow correlation functions. The first source of error can be largely eliminated by twist averaging. If the simulation cell is large enough that XC hole does not “leak” out of the simulation cell, the second source can be eliminated either through use of the MPC interaction or the a postiori correction of Chiesa et al.
The satisfaction of the leakage requirement is controlled by whether the minimum distance, \(L_{\text{min}}\), from one supercell image to the next is greater than the width of the XC hole. Therefore, given a choice, it is best to use a cell that is as nearly cubic as possible since this choice maximizes \(L_{\text{min}}\) for a given number of atoms. Most often, however, the primitive cell is not cubic. In these cases, if we wish to choose the optimal supercell to reduce finite-size effects, we cannot use the simple primitive tiling scheme. In the generalized scheme we present, it is possible to choose far better supercells (from the standpoint of finite-size errors), while retaining the storage efficiency of the original tiling scheme.
The mathematics
Consider the set of primitive lattice vectors, \(\{\mathbf{a}^{\text{p}}_1, \mathbf{a}^{\text{p}}_2, \mathbf{a}^{\text{p}}_3\}\). We may write these vectors in a matrix, \(\mathbf{L}_p\), whose rows are the primitive lattice vectors. Consider a nonsingular matrix of integers, \(\mathbf{S}\). A corresponding set of supercell lattice vectors, \(\{\mathbf{a}^{\text{s}}_1, \mathbf{a}^{\text{s}}_2, \mathbf{a}^{\text{s}}_3\}\), can be constructed by the matrix product
If the primitive cell contains \(N_p\) atoms, the supercell will then contain \(N_s = |\det(\mathbf{S})| N_p\) atoms.
Example: FeO
As an example, consider the primitive cell for antiferromagnetic FeO (wustite) in the rocksalt structure. The primitive vectors, given in units of the lattice constant, are given by
This primitive cell contains two iron atoms and two oxygen atoms. It is a very elongated cell with acute angles and, thus, has a short minimum distance between adjacent images.
The smallest cubic cell consistent with the AFM ordering can be constructed with the matrix
This cell has \(2|\det(\mathbf{S})| = 32\) iron atoms and 32 oxygen atoms. In this example, we may perform the simulation in the 32-iron supercell, while storing the orbitals only in the 2-iron primitive cell, for a savings of a factor of 16.
The k-point mesh
To be able to use the generalized tiling scheme, we need to have the appropriate number of bands to occupy in the supercell. This may be achieved by appropriately choosing the k-point mesh. In this section, we explain how these points are chosen.
For simplicity, let us assume that the supercell calculation will be performed at the \(\Gamma\)-point. We can easily lift this restriction later. The fact that supercell calculation is performed at \(\Gamma\) implies that the k-points used in the primitive-cell calculation must be \(\mathbf{G}\)-vectors of the superlattice. This still leaves us with an infinite set of vectors. We may reduce this set to a finite number by considering that the orbitals must form a linearly independent set. Orbitals with k-vectors \(\mathbf{k}^p_1\) and \(\mathbf{k}^p_2\) will differ by at most a constant factor of \(\mathbf{k}^p_1 - \mathbf{k}^p_2 = \mathbf{G}^p\), where \(\mathbf{G}^p\) is a reciprocal lattice vector of the primitive cell.
Combining these two considerations gives us a prescription for generating our k-point mesh. The mesh may be taken to be the set of k-point which are G-vectors of the superlattice, reside within the first Brillouin zone (FBZ) of the primitive lattice, whose members do not differ a G-vector of the primitive lattice. Upon constructing such a set, we find that the number of included k-points is equal to \(|\det(\mathbf{S})|\), precisely the number we need. This can by considering the fact that the supercell has a volume \(|\det(\mathbf{S})|\) times that of the primitive cell. This implies that the volume of the supercell’s FBZ is \(|\det(\mathbf{S})|^{-1}\) times that of the primitive cell. Hence, \(|\det(\mathbf{S})|\) G-vectors of the supercell will fit in the FBZ of the primitive cell. Removing duplicate k-vectors, which differ from another by a reciprocal lattice vector, avoids double-counting vectors that lie on zone faces.
Formulae
Let \(\mathbf{A}\) be the matrix whose rows are the direct lattice vectors, \(\{\mathbf{a}_i\}\). Then, let the matrix \(\mathbf{B}\) be defined as \(2\pi(\mathbf{A}^{-1})^\dagger\). Its rows are the primitive reciprocal lattice vectors. Let \(\mathbf{A}_p\) and \(\mathbf{A}_s\) represent the primitive and superlattice matrices, respectively, and similarly for their reciprocals. Then we have
Consider a k-vector, \(\mathbf{k}\). It may alternatively be written in basis of reciprocal lattice vectors as \(\mathbf{t}\).
We may then express a twist vector of the primitive lattice, \(\mathbf{t}_p\), in terms of the superlattice.
This gives the simple result that twist vectors transform in precisely the same way as direct lattice vectors.
Feature: Hybrid orbital representation
where \(u_{lm}(r)\) are complex radial functions represented in some radial basis (e.g., splines).
Real spherical harmonics
If \(\phi(\mathbf{r})\) can be written as purely real, we can change the representation so that
where \(\bar{Y}_\ell^m\) are the real spherical harmonics defined by
We need then to relate \(\bar{u}_{\ell m}\) to \(u_{\ell m}\). We wish to express
in terms of \(\bar{u}_{\ell m}(r)\) and \(Y_{\ell m}\).
For \(m>0\),
For \(m<0\),
Then for \(m > 0\),
Projecting to atomic orbitals
Inside a muffin tin, orbitals are represented as products of spherical harmonics and 1D radial functions, primarily represented by splines. For a muffin tin centered at \(\mathbf{I}\),
Let use consider the case that our original representation for \(\phi(\mathbf{r})\) is of the form
Recall that
Conjugating,
Setting \(\mathbf{k}\rightarrow -k\),
Then,
Then
Comparing with (229),
If we had adopted the opposite sign convention for Fourier transforms (as is unfortunately the case in wfconvert), we would have
Feature: Electron-electron-ion Jastrow factor
The general form of the 3-body Jastrow we describe here depends on the three interparticle distances, \((r_{ij}, r_{iI}, r_{jI})\).
Note that we constrain the form of \(U\) such that \(U(r_{ij}, r_{iI},r_{jI}) = U(r_{ij}, r_{jI},r_{iI})\) to preserve the particle symmetry of the wavefunction. We then compute the gradient as
To compute the Laplacian, we take
We now wish to compute the gradient of these terms w.r.t. the ion position, \(I\).
For the gradient w.r.t. \(i\) of the gradient w.r.t. \(I\), the result is a tensor:
For the Laplacian,
Feature: Reciprocal-space Jastrow factors
Two-body Jastrow
This may be rewritten as
The \(-1\) is just a constant term and may be subsumed into the \(a_\mathbf{G}\) coefficient by a simple redefinition. This leaves a simple, but general, form:
We may now further constrain this on physical grounds. First, we recognize that \(J_2\) should be real. Since \(\rho_{-\mathbf{G}} = \rho_\mathbf{G}^*\), it follows that \(\rho_{\mathbf{G}}\rho_{-\mathbf{G}} = |\rho_\mathbf{G}|^2\) is real, so that \(a_\mathbf{G}\) must be real. Furthermore, we group the \(\mathbf{G}\)’s into \((+\mathbf{G}, -\mathbf{G})\) pairs and sum over only the positive vectors to save time.
One-body Jastrow
The 1-body Jastrow has a similar form but depends on the displacement from the electrons to the ions in the system.
where \(\alpha\) denotes the different ionic species. We may rewrite this in terms of \(\rho^{\alpha}_\mathbf{G}\):
where
We note that in the preceding equation, for a single configuration of the ions, the sum in brackets can be rewritten as a single constant. This implies that the per-species 1-body coefficients, \(b^\alpha_\mathbf{G}\), are underdetermined for single configuration of the ions. In general, if we have \(N\) species, we need \(N\) linearly independent ion configurations to uniquely determine \(b^{\alpha}_\mathbf{G}\). For this reason, we will drop the \(\alpha\) superscript of \(b_\mathbf{G}\) for now.
If we do desire to find a reciprocal space 1-body Jastrow that is transferable to systems with different ion positions and \(N\) ionic species, we must perform compute \(b_\mathbf{G}\) for \(N\) different ion configurations. We may then construct \(N\) equations at each value of \(\mathbf{G}\) to solve for the \(N\) unknown values, \(b^\alpha_\mathbf{G}\).
In the 2-body case, \(a_\mathbf{G}\) was constrained to be real by the fact that \(\rho_\mathbf{G}\rho_{-\mathbf{G}}\) was real. However, in the 1-body case, there is no such guarantee about \(\rho^\alpha_\mathbf{G}\rho_\mathbf{G}\). Therefore, in general, \(b_\mathbf{G}\) may be complex.
Symmetry considerations
For a crystal, many of the \(\mathbf{G}\)-vectors will be equivalent by symmetry. It is useful then to divide the \(\mathbf{G}\)-vectors into symmetry-related groups and then require that they share a common coefficient. Two vectors, \(\mathbf{G}\) and \(\mathbf{G}'\), may be considered to be symmetry related if, for all \(\alpha\) and \(\beta\)
For the 1-body term, we may also omit from our list of \(\mathbf{G}\)-vectors those for which all species structure factors are zero. This is equivalent to saying that if we are tiling a primitive cell we should include only the \(\mathbf{G}\)-vectors of the primitive cell and not the supercell. Note that this is not the case for the 2-body term since the XC hole should not have the periodicity of the primitive cell.
Gradients and Laplacians
The Laplacian is then given by