Lab 3: Advanced molecular calculations
Topics covered in this lab
This lab covers molecular QMC calculations with wavefunctions of increasing sophistication. All of the trial wavefunctions are initially generated with the GAMESS code. Topics covered include:
Generating single-determinant trial wavefunctions with GAMESS (HF and DFT)
Generating multideterminant trial wavefunctions with GAMESS (CISD, CASCI, and SOCI)
Optimizing wavefunctions (Jastrow factors and CSF coefficients) with QMC
DMC time step and walker population convergence studies
Systematic progressions of Jastrow factors in VMC
Systematic convergence of DMC energies with multideterminant wavefunctions
Influence of orbitals basis choice on DMC energy
Lab directories and files
abs/lab3_advanced_molecules/exercises
│
├── ex1_first-run-hartree-fock - basic work flow from Hatree-Fock to DMC
│ ├── gms - Hatree-Fock calculation using GAMESS
│ │ ├── h2o.hf.inp - GAMESS input
│ │ ├── h2o.hf.dat - GAMESS punch file containing orbitals
│ │ └── h2o.hf.out - GAMESS output with orbitals and other info
│ ├── convert - Convert GAMESS wavefunction to QMCPACK format
│ │ ├── h2o.hf.out - GAMESS output
│ │ ├── h2o.ptcl.xml - converted particle positions
│ │ └── h2o.wfs.xml - converted wave function
│ ├── opt - VMC optimization
│ │ └── optm.xml - QMCPACK VMC optimization input
│ ├── dmc_timestep - Check DMC timestep bias
│ │ └── dmc_ts.xml - QMCPACK DMC input
│ └── dmc_walkers - Check DMC population control bias
│ └── dmc_wk.xml - QMCPACK DMC input template
│
├── ex2_slater-jastrow-wf-options - explore jastrow and orbital options
│ ├── jastrow - Jastrow options
│ │ ├── 12j - no 3-body Jastrow
│ │ ├── 1j - only 1-body Jastrow
│ │ └── 2j - only 2-body Jastrow
│ └── orbitals - Orbital options
│ ├── pbe - PBE orbitals
│ │ └── gms - DFT calculation using GAMESS
│ │ └── h2o.pbe.inp - GAMESS DFT input
│ ├── pbe0 - PBE0 orbitals
│ ├── blyp - BLYP orbitals
│ └── b3lyp - B3LYP orbitals
│
├── ex3_multi-slater-jastrow
│ ├── cisd - CISD wave function
│ │ ├── gms - CISD calculation using GAMESS
│ │ │ ├── h2o.cisd.inp - GAMESS input
│ │ │ ├── h2o.cisd.dat - GAMESS punch file containing orbitals
│ │ │ └── h2o.cisd.out - GAMESS output with orbitals and other info
│ │ └── convert - Convert GAMESS wavefunction to QMCPACK format
│ │ └── h2o.hf.out - GAMESS output
│ ├── casci - CASCI wave function
│ │ └── gms - CASCI calculation using GAMESS
│ └── soci - SOCI wave function
│ ├── gms - SOCI calculation using GAMESS
│ ├── thres0.01 - VMC optimization with few determinants
│ └── thres0.0075 - VMC optimization with more determinants
│
└── pseudo
├── H.BFD.gamess - BFD pseudopotential for H in GAMESS format
├── O.BFD.CCT.gamess - BFD pseudopotential for O in GAMESS format
├── H.xml - BFD pseudopotential for H in QMCPACK format
└── O.xml - BFD pseudopotential for H in QMCPACK format
Exercise #1: Basics
The purpose of this exercise is to show how to generate wavefunctions for QMCPACK using GAMESS and to optimize the resulting wavefunctions using VMC. This will be followed by a study of the time step and walker population dependence of DMC energies. The exercise will be performed on a water molecule at the equilibrium geometry.
Generation of a Hartree-Fock wavefunction with GAMESS
From the top directory, go to “ex1_first-run-hartree-fock/gms.” This
directory contains an input file for a HF calculation of a water
molecule using BFD ECPs and the corresponding cc-pVTZ basis set. The
input file should be named: “h2o.hf.inp.” Study the input file. See
Section Appendix A: GAMESS input for a
more detailed description of the GAMESS input syntax. However, there
will be a better time to do this soon, so we recommend continuing with
the exercise at this point. After you are done, execute GAMESS with this
input and store the standard output in a file named “h2o.hf.output.”
Finally, in the “convert” folder, use convert4qmc to generate the
QMCPACK particleset and wavefunction files. It is always useful
to rename the files generated by convert4qmc to something meaningful
since by default they are called sample.Gaussian-G2.xml and
sample.Gaussian-G2.ptcl.xml. In a standard computer (without
cross-compilation), these tasks can be accomplished by the following
commands.
cd ${TRAINING TOP}/ex1_first-run-hartree-fock/gms
jobrun_vesta rungms h2o.hf
cd ../convert
cp ../gms/h2o.hf.output
jobrun_vesta convert4qmc -gamess h2o.hf.output -add3BodyJ
mv sample.Gaussian-G2.xml h2o.wfs.xml
mv sample.Gaussian-G2.ptcl.xml h2o.ptcl.xml
The HF energy of the system is -16.9600590022 Ha. To search for the energy in the output file quickly, you can use
grep "TOTAL ENERGY =" h2o.hf.output
As the job runs on VESTA, it is a good time to review Section :ref`lab-adv-mol-convert4qmc`, “Appendix B: convert4qmc,” which contains a description on the use of the converter.
Optimize the wavefunction
When execution of the previous steps is completed, there should be two
new files called h2o.wfs.xml and h2o.ptcl.xml. Now we will use
VMC to optimize the Jastrow parameters in the wavefunction. From the top
directory, go to “ex1_first-run-hartree-fock/opt.” Copy the xml
files generated in the previous step to the current directory. This
directory should already contain a basic QMCPACK input file for an
optimization calculation (optm.xml) Open optm.xml with your
favorite text editor and modify the name of the files that contain the
wavefunction and particleset XML blocks. These files are
included with the commands:
<include href=ptcl.xml/>
<include href=wfs.xml/>
(the particle set must be defined before the wavefunction). The name of
the particle set and wavefunction files should now be h2o.ptcl.xml
and h2o.wfs.xml, respectively. Study both files and submit when you
are ready. Notice that the location of the ECPs has been set for you; in
your own calculations you have to make sure you obtain the ECPs from the
appropriate libraries and convert them to QMCPACK format using
ppconvert. While these calculations finish is a good time to study
Appendix C: Wavefunction optimization XML block, which contains a review of the main parameters
in the optimization XML block. The previous steps can be accomplished by
the following commands:
cd ${TRAINING TOP}/ex1_first-run-hartree-fock/opt
cp ../convert/h2o.wfs.xml ./
cp ../convert/h2o.ptcl.xml ./
# edit optm.xml to include the correct ptcl.xml and wfs.xml
jobrun_vesta qmcpack optm.xml
Use the analysis tool qmca to analyze the results of the
calculation. Obtain the VMC energy and variance for each step in the
optimization and plot it using your favorite program. Remember that
qmca has built-in functions to plot the analyzed data.
qmca -q e *scalar.dat -p
The resulting energy as a function of the optimization step should look
qualitatively similar to Fig. 19. The energy should
decrease quickly as a function of the number of optimization steps.
After 6–8 steps, the energy should be converged to \(\sim\)2–3
mHa. To improve convergence, we would need to increase the number of
samples used during optimization (You can check this for yourself
later.). With optimized wavefunctions, we are in a position to perform
VMC and DMC calculations. The modified wavefunction files after each
step are written in a file named ID.sNNN.opt.xml, where ID is the
identifier of the calculation defined in the input file (this is defined
in the project XML block with parameter “id”) and NNN is a series number
that increases with every executable xml block in the input file.
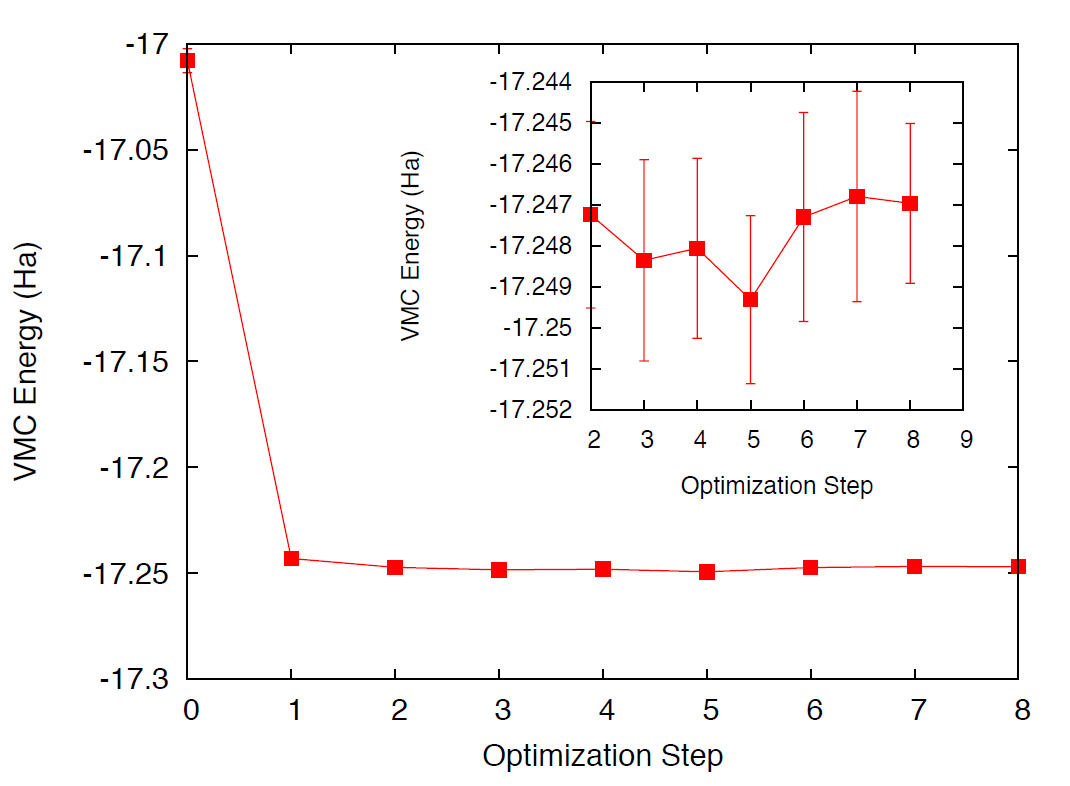
Fig. 19 VMC energy as a function of optimization step.
Time-step study
Now we will study the dependence of the DMC energy with time step. From
the top directory, go to “ex1_first-run-hartree-fock/dmc_timestep.”
This folder contains a basic XML input file (dmc_ts.xml) that
performs a short VMC calculation and three DMC calculations with varying
time steps (0.1, 0.05, 0.01). Link the particleset and the last
optimization file from the previous folder (the file called
jopt-h2o.sNNN.opt.xml with the largest value of NNN). Rename the
optimized wavefunction file to any suitable name if you wish (for
example, h2o.opt.xml) and change the name of the particleset and
wavefunction files in the input file. An optimized wavefunction can
be found in the reference files (same location) in case it is needed.
The main steps needed to perform this exercise are:
cd \$\{TRAINING TOP\}/ex1_first-run-hartree-fock/dmc_timestep
cp ../opt/h2o.ptcl.xml ./
cp ../opt/jopt-h2o.s007.opt.xml h2o.opt.wfs.xml
# edit dmc_ts.xml to include the correct ptcl.xml and wfs.xml
jobrun_vesta qmcpack dmc_ts.xml
While these runs complete, go to Appendix D: VMC and DMC XML block and review the basic VMC and DMC input blocks. Notice that in the current DMC blocks the time step is decreased as the number of blocks is increased. Why is this?
When the simulations are finished, use qmca to analyze the output
files and plot the DMC energy as a function of time step. Results should
be qualitatively similar to those presented in
Fig. 20; in this case we present more time
steps with well converged results to better illustrate the time step
dependence. In realistic calculations, the time step must be chosen
small enough so that the resulting error is below the desired accuracy.
Alternatively, various calculations can be performed and the results
extrapolated to the zero time-step limit.
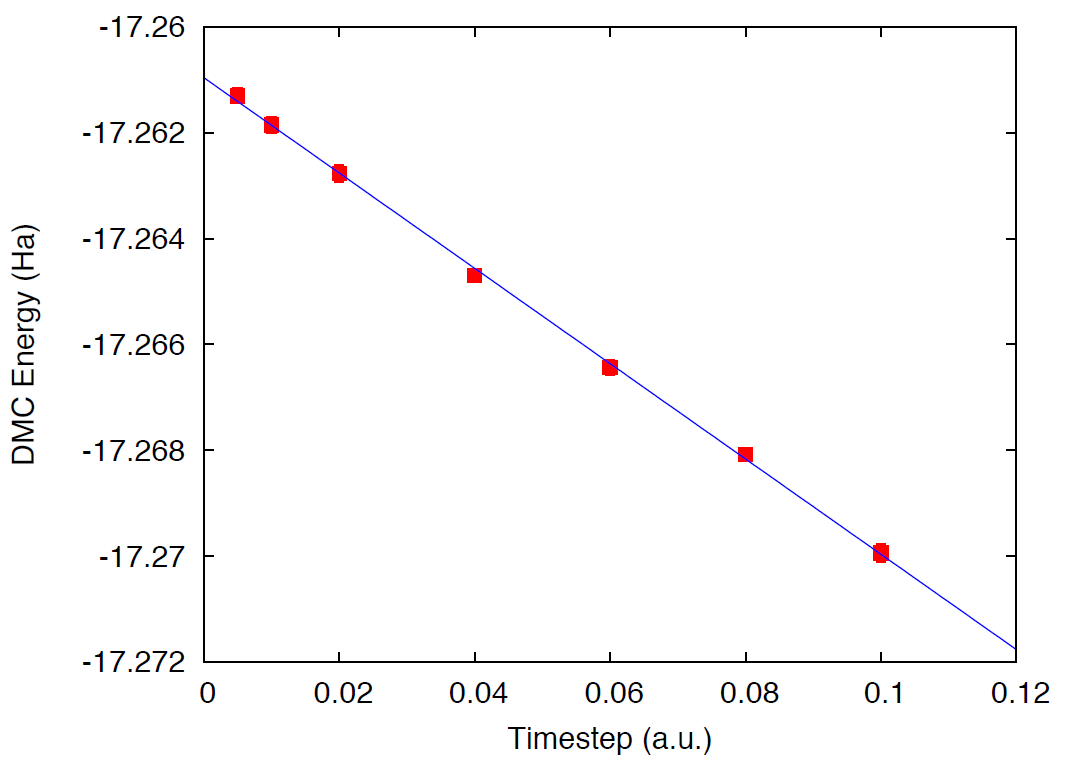
Fig. 20 DMC energy as a function of time step.
Walker population study
Now we will study the dependence of the DMC energy with the number of walkers in the simulation. Remember that, in principle, the DMC distribution is reached in the limit of an infinite number of walkers. In practice, the energy and most properties converge to high accuracy with \(\sim\)100–1,000 walkers. The actual number of walkers needed in a calculation will depend on the accuracy of the VMC wavefunction and on the complexity and size of the system. Also notice that using too many walkers is not a problem; at worse it will be inefficient since it will cost more computer time than necessary. In fact, this is the strategy used when running QMC calculations on large parallel computers since we can reduce the statistical error bars efficiently by running with large walker populations distributed across all processors.
From the top directory, go to
“ex1_first-run-hartree-fock/dmc_walkers.” Copy the optimized
wavefunction and particleset files used in the previous
calculations to the current folder; these are the files generated during
step 2 of this exercise. An optimized wavefunction file can be found
in the reference files (same location) in case it is needed. The
directory contains a sample DMC input file and submission script. Create
three directories named NWx, with x values of 120,240,480, and copy the
input file to each one. Go to “NW120,” and, in the input file, change
the name of the wavefunction and particleset files (in this case
they will be located one directory above, so use
“../dmc_timestep/h2.opt.xml,” for example); change the PP directory
so that it points to one directory above; change “targetWalkers” to 120;
and change the number of steps to 100, the time step to 0.01, and the
number of blocks to 400. Notice that “targetWalkers” is one way to set
the desired (average) number of walkers in a DMC calculation. One can
alternatively set “samples” in the <qmc method="vmc" block to carry over de-correlated VMC
configurations as DMC walkers. For your own simulations, we generally
recommend setting \(\sim\)2*(#threads) walkers per node (slightly
smaller than this value).
The main steps needed to perform this exercise are
cd ${TRAINING TOP}/ex1_first-run-hartree-fock/dmc_walkers
cp ../opt/h2o.ptcl.xml ./
cp ../opt/jopt-h2o.s007.opt.xml h2o.opt.wfs.xml
# edit dmc_wk.xml to include the correct ptcl.xml and wfs.xml and
# use the correct pseudopotential directory
mkdir NW120
cp dmc_wk.xml NW120
# edit dmc_wk.xml to use the desired number of walkers,
# and collect the desired amount of statistics
jobrun_vesta qmcpack dmc_wk.xml
# repeat for NW240, NW480
Repeat the same procedure in the other folders by setting
(targetWalkers=240, steps=100, timestep=0.01, blocks=200) in NW240 and
(targetWalkers=480, steps=100, timestep=0.01, blocks=100) in NW480. When
the simulations complete, use qmca to analyze and plot the energy as
a function of the number of walkers in the calculation. As always,
Fig. 21 shows representative results of the
energy dependence on the number of walkers for a single water molecule.
As shown, less than 240 walkers are needed to obtain an accuracy of 0.1
mHa.
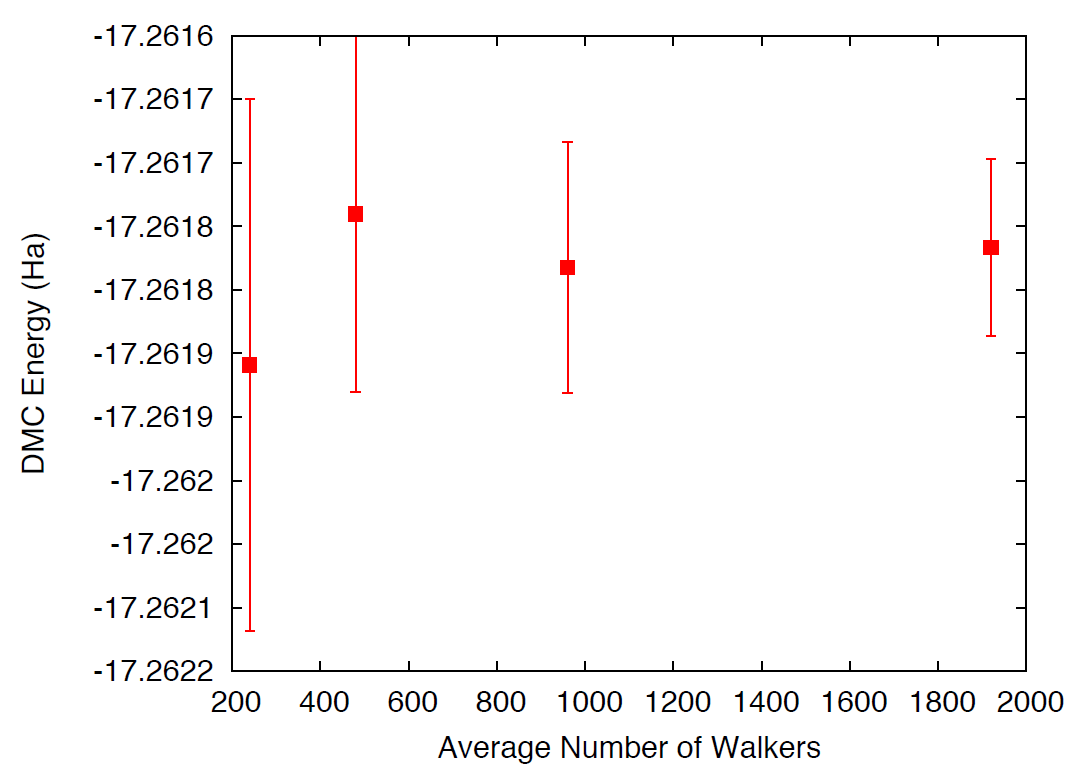
Fig. 21 DMC energy as a function of the average number of walkers.
Exercise #2: Slater-Jastrow wavefunction options
From this point on in the tutorial we assume familiarity with the basic
parameters in the optimization, VMC, and DMC XML input blocks of
QMCPACK. In addition, we assume familiarity with the submission system.
As a result, the folder structure will not contain any prepared input or
submission files, so you will need to generate them using input files
from exercise 1. In the case of QMCPACK sample files, you will find
optm.xml, vmc dmc.xml, and submit.csh files. Some of the
options in these files can be left unaltered, but many of them will need
to be tailored to the particular calculation.
In this exercise we will study the dependence of the DMC energy on the choices made in the wavefunction ansatz. In particular, we will study the influence/dependence of the VMC energy with the various terms in the Jastrow. We will also study the influence of the VMC and DMC energies on the SPOs used to form the Slater determinant in single-determinant wavefunctions. For this we will use wavefunctions generated with various exchange-correlation functionals in DFT. Finally, we will optimize a simple multideterminant wavefunction and study the dependence of the energy on the number of configurations used in the expansion. All of these exercises will be performed on the water molecule at equilibrium.
Influence of Jastrow on VMC energy with HF wavefunction
In this section we will study the dependence of the VMC energy on the
various Jastrow terms (e.g., 1-body, 2-body and 3-body. From the top
directory, go to “ex2_slater-jastrow-wf-options/jastrow.” We will
compare the single-determinant VMC energy using a 2-body Jastrow term,
both 1- and 2-body terms, and finally 1-, 2- and 3-body terms. Since we
are interested in the influence of the Jastrow, we will use the HF
orbitals calculated in exercise #1. Make three folders named 2j, 12j,
and 123j. For both 2j and 12j, copy the input file optm.xml from
“ex1_first-run-hartree-fock/opt.” This input file performs both
wavefunction optimization and a VMC calculation. Remember to correct
relative paths to the PP directory. Copy the un-optimized HF
wavefunction and particleset files from
“ex1_first-run-hartree-fock/convert”; if you followed the
instructions in exercise #1 these should be named h2o.wfs.xml and
h2o.ptcl.xml. Otherwise, you can obtained them from the REFERENCE
files. Modify the h2o.wfs.xml file to remove the appropriate Jastrow
blocks. For example, for a 2-body Jastrow (only), you need to eliminate
the Jastrow blocks named <jastrow name="J1" and <jastrow name="J3." In
the case of 12j, remove only <jastrow name="J3." Recommended settings
for the optimization run are nodes=32, threads=16, blocks=250,
samples=128000, time-step=0.5, 8 optimization loops. Recommended
settings in the VMC section are walkers=16, blocks=1000, steps=1,
substeps=100. Notice that samples should always be set to blocks*threads
per node*nodes = 32*16*250=128000. Repeat the process in both 2j and 12j
cases. For the 123j case, the wavefunction has already been optimized in
the previous exercise. Copy the optimized HF wavefunction and the
particleset from “ex1_first-run-hartree-fock/opt.” Copy the input
file from any of the previous runs and remove the optimization block
from the input, just leave the VMC step. In all three cases, modify the
submission script and submit the run.
Because these simulations will take several minutes to complete, this is
an excellent opportunity to go to
Appendix E: Wavefunction XML block and review the wavefunction XML block used by QMCPACK. When the
simulations are completed, use qmca to analyze the output files.
Using your favorite plotting program (e.g., gnu plot), plot the energy
and variance as a function of the Jastrow form.
Fig. 22 shows a typical result for this
calculation. As can be seen, the VMC energy and variance depends
strongly on the form of the Jastrow. Since the DMC error bar is directly
related to the variance of the VMC energy, improving the Jastrow will
always lead to a reduction in the DMC effort. In addition, systematic
approximations (time step, number of walkers, etc.) are also reduced
with improved wavefunctions.
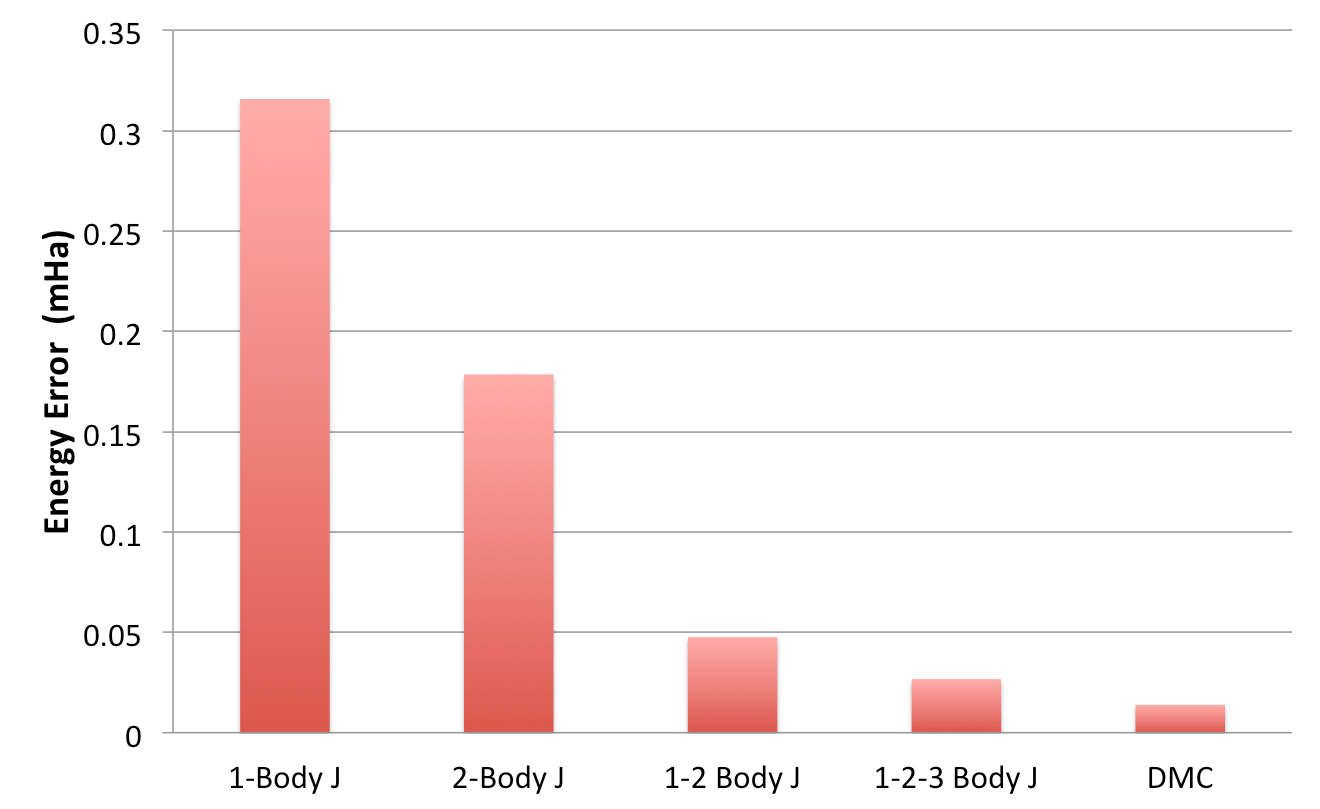
Fig. 22 VMC energy as a function of Jastrow type.
Generation of wavefunctions from DFT using GAMESS
In this section we will use GAMESS to generate wavefunctions for QMCPACK
from DFT calculations. From the top folder, go to
“ex2_slater-jastrow-wf-options/orbitals.” To demonstrate the
variation in DMC energies with the choice of DFT orbitals, we will
choose the following set of exchange-correlation functionals (PBE, PBE0,
BLYP, B3LYP). For each functional, make a directory using your preferred
naming convention (e.g., the name of the functional). Go into each
folder and copy a GAMESS input file from
“ex1_first-run-hartree-fock/gms.” Rename the file with your
preferred naming convention; we suggest using h2o.[dft].inp, where
[dft] is the name of the functional used in the calculation. At this
point, this input file should be identical to the one used to generate
the HF wavefunction in exercise #1. To perform a DFT calculation we only
need to add “DFTTYP” to the $CONTRL ... $END section and set it to the desired functional
type, for example, “DFTTYP=PBE” for a PBE functional. This variable must
be set to (PBE, PBE0, BLYP, B3LYP) to obtain the appropriate functional
in GAMESS. For a complete list of implemented functionals, see the
GAMESS input manual.
Optimization and DMC calculations with DFT wavefunctions
In this section we will optimize the wavefunction generated in the
previous step and perform DMC calculations. From the top directory, go
to “ex2_slater-jastrow-wf-options/orbitals.” The steps required to
achieve this are identical to those used to optimize the wavefunction
with HF orbitals. Make individual folders for each calculation and
obtain the necessary files to perform optimization, for example, VMC and
DMC calculations from “for ex1_first-run-hartree-fock/opt” and
“ex1_first-run-hartree-fock/dmc_ts.” For each functional, make the
appropriate modifications to the input files and copy the
particleset and wavefunction files from the appropriate
directory in “ex2_slater-jastrow-wf-options/orbitals/[dft].” We
recommend the following settings: nodes=32, threads=16, (in
optimization) blocks=250, samples=128000, timestep=0.5, 8 optimization
loops, (in VMC) walkers=16, blocks=100, steps=1, substeps=100, (in DMC)
blocks 400, targetWalkers=960, and timestep=0.01. Submit the runs and
analyze the results using qmca.
How do the energies compare against each other? How do they compare against DMC energies with HF orbitals?
Exercise #3: Multideterminant wavefunctions
In this exercise we will study the dependence of the DMC energy on the set of orbitals and the type of configurations included in a multideterminant wavefunction.
Generation of a CISD wavefunctions using GAMESS
In this section we will use GAMESS to generate a multideterminant wavefunction with configuration interaction with single and double excitations (CISD). In CISD, the Schrodinger equation is solved exactly on a basis of determinants including the HF determinant and all its single and double excitations.
Go to “ex3_multi-slater-jastrow/cisd/gms” and you will see input and
output files named h2o.cisd.inp and h2o.cisd.out. Because of
technical problems with GAMESS in the BGQ architecture of VESTA, we are
unable to use CISD properly in GAMESS. Consequently, the output of the
calculation is already provided in the directory.
There will be time in the next step to study the GAMESS input files and the description in Appendix A: GAMESS input. Since the output is already provided, the only action needed is to use the converter to generate the appropriate QMCPACK files.
jobrun_vesta convert4qmc h2o.cisd.out -ci h2o.cisd.out \
-readInitialGuess 57 -threshold 0.0075
We used the PRTMO=.T. flag in the GUESS section to include orbitals in
the output file. You should read these orbitals from the output
(-readInitialGuess 40). The highest occupied orbital in any determinant
should be 34, so reading 40 orbitals is a safe choice. In this case, it
is important to rename the XML files with meaningful names, for example,
h2o.cisd.wfs.xml. A threshold of 0.0075 is sufficient for the
calculations in the training.
Optimization of a multideterminant wavefunction
In this section we will optimize the wavefunction generated in the
previous step. There is no difference in the optimization steps if a
single determinant and a multideterminant wavefunction. QMCPACK will
recognize the presence of a multideterminant wavefunction and will
automatically optimize the linear coefficients by default. Go to
“ex3_multi-slater-jastrow/cisd” and make a folder called
thres0.01. Copy the particleset and wavefunction files
created in the previous step to the current directory. With your
favorite text editor, open the wavefunction file h2o.wfs.xml.
Look for the multideterminant XML block and change the “cutoff”
parameter in detlist to 0.01. Then follow the same steps used in Section
9.4.3, “Optimization and DMC calculations with DFT wavefunctions” to
optimize the wavefunction. Similar to this case, design a QMCPACK input
file that performs wavefunction optimization followed by VMC and DMC
calculations. Submit the calculation.
This is a good time to review the GAMESS input file description in
Appendix A: GAMESS input, go to the previous directory and make a new folder
named thres0.0075. Repeat the previous steps to optimize the
wavefunction with a cutoff of 0.01, but use a cutoff of 0.0075 this
time. This will increase the number of determinants used in the
calculation. Notice that the “cutoff” parameter in the XML should be
less than the “-threshold 0.0075” flag passed to the converted, which is
further bounded by the PRTTOL flag in the GAMESS input.
After the wavefunction is generated, we are ready to optimize. Instead of starting from an un-optimized wavefunction, we can start from the optimized wavefunction from thres0.01 to speed up convergence. You will need to modify the file and change the cutoff in detlist to 0.0075 with a text editor. Repeat the optimization steps and submit the calculation.
When you are done, use qmca to analyze the results. Compare the energies at these two
coefficient cutoffs with the energies obtained with DFT orbitals. Because of the time limitations of this tutorial, it is not practical to optimize the wavefunctions with a smaller cutoff since this would require more samples and longer runs due to the larger number of optimizable parameters. Fig. 23 shows the results of such exercise: the DMC energy as a function of the cutoff in the wavefunction. As can be seen, a large improvement in the energy is obtained as the number of configurations is increased.
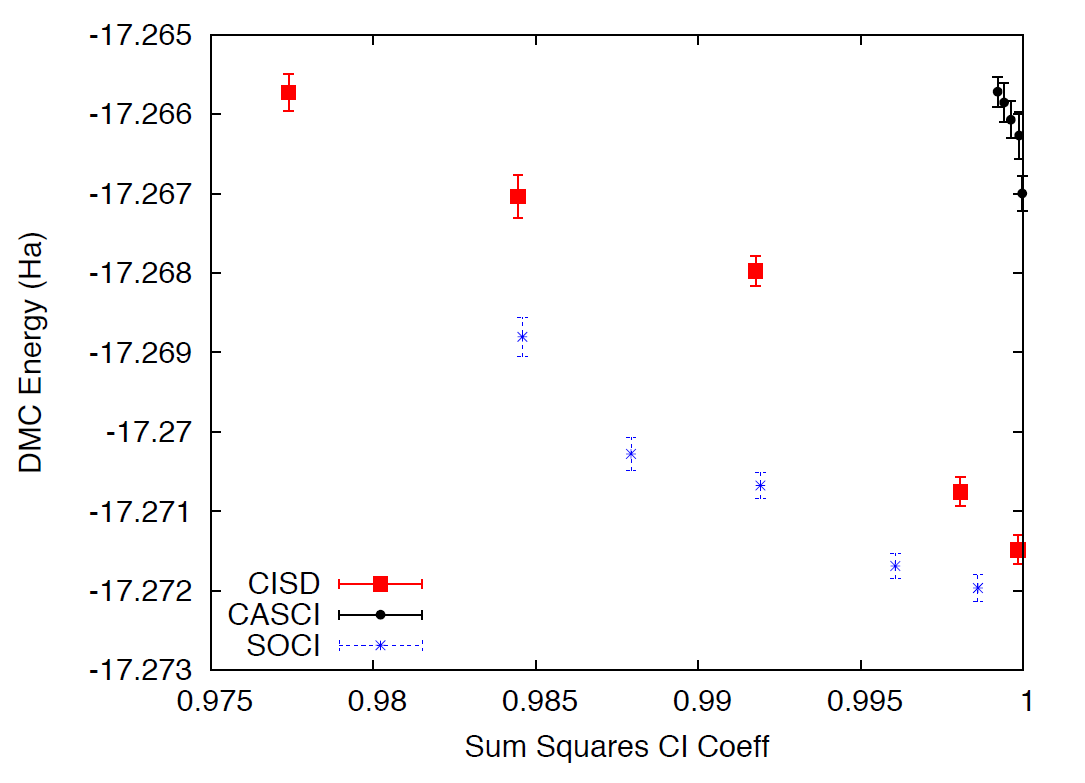
Fig. 23 DMC energy as a function of the sum of the square of CI coefficients from CISD.
CISD, CASCI, and SOCI
Go to “ex3_multi-slater-jastrow” and inspect the folders for the
remaining wavefunction types: CASCI and SOCI. Follow the steps in the
previous exercise and obtain the optimized wavefunctions for these
determinant choices. Notice that the SOCI GAMESS output is not included
because it is large. Already converted XML inputs can be found in
“ex3_multi-slater-jastrow/soci/thres*.”
A CASCI wavefunction is produced from a CI calculation that includes all the determinants in a complete active space (CAS) calculation, in this case using the orbitals from a previous CASSCF calculation. In this case we used a CAS(8,8) active space that includes all determinants generated by distributing 8 electrons in the lowest 8 orbitals. A SOCI calculation is similar to the CAS-CI calculation, but in addition to the determinants in the CAS it also includes all single and double excitations from all of them, leading to a much larger determinant set. Since you now have considerable experience optimizing wavefunctions and calculating DMC energies, we will leave it to you to complete the remaining tasks on your own. If you need help, refer to previous exercises in the tutorial. Perform optimizations for both wavefunctions using cutoffs in the CI expansion of 0.01 an 0.0075. If you have time, try to optimize the wavefunctions with a cutoff of 0.005. Analyze the results and plot the energy as a function of cutoff for all three cases: CISD, CAS-CI, and SOCI.
Fig. 23 shows the result of similar calculations using more samples and smaller cutoffs. The results should be similar to those produced in the tutorial. For reference, the exact energy of the water molecule with ECPs is approximately -17.276 Ha. From the results of the tutorial, how does the selection of determinants relate to the expected DMC energy? What about the choice in the set of orbitals?
Appendix A: GAMESS input
In this section we provide a brief description of the GAMESS input needed to produce
trial wavefunction for QMC calculations with QMCPACK. We assume basic familiarity
with GAMESS input structure, particularly regarding the input of atomic coordinates and
the definition of Gaussian basis sets. This section focuses on generation of the output
files needed by the converter tool, convert4qmc. For a description of the converter, see Appendix B: convert4qmc.
Only a subset of the methods available in GAMESS can be used to generate wavefunctions for QMCPACK, and we restrict our description to these. For a complete description of all the options and methods available in GAMESS, please refer to the official documentation at “http://www.msg.ameslab.gov/gamess/documentation.html.”
Currently, convert4qmc can process output for the following methods in GAMESS (in
SCFTYP): RHF, ROHF, and MCSCF. Both HF and DFT calculations (any DFT
type) can be used in combination with RHF and ROHF calculations. For MCSCF and CI
calculations, ALDET, ORMAS, and GUGA drivers can be used (details follow).
HF input
The following input will perform a restricted HF calculation on a closed-shell singlet
(multiplicity=1). This will generate RHF orbitals for any molecular system defined in
$DATA ... $END.
$CONTRL SCFTYP=RHF RUNTYP=ENERGY MULT=1
ISPHER=1 EXETYP=RUN COORD=UNIQUE MAXIT=200 $END
$SYSTEM MEMORY=150000000 $END
$GUESS GUESS=HUCKEL $END
$SCF DIRSCF=.TRUE. $END
$DATA
...
Atomic Coordinates and basis set
...
$END
Main options:
SCFTYP: Type of SCF method, options: RHF, ROHF, MCSCF, UHF and NONE.
RUNTYP: Type of run. For QMCPACK wavefunction generation this should always be ENERGY.
MULT: Multiplicity of the molecule.
ISPHER: Use spherical harmonics (1) or Cartesian basis functions (-1).
COORD: Input structure for the atomic coordinates in $DATA.
DFT calculations
The main difference between the input for a RHF/ROHF calculation and a DFT calculation is the definition of the DFTTYP parameter. If this is set in the $CONTROL section, a DFT calculation will be performed with the appropriate functional. Notice that although the default values are usually adequate, DFT calculations have many options involving the integration grids and accuracy settings. Make sure you study the input manual to be aware of these. Refer to the input manual for a list of the implemented exchange-correlation functionals.
MCSCF
MCSCF calculations are performed by setting SCFTYP=MCSCF in the CONTROL section. If this option is set, an MCSCF section must be added to the input file with the options for the calculation. An example section for the water molecule used in the tutorial follows.
$MCSCF CISTEP=GUGA MAXIT=1000 FULLNR=.TRUE. ACURCY=1.0D-5 $END
The most important parameter is CISTEP, which defines the CI package used. The only options compatible with QMCPACK are: ALDET, GUGA, and ORMAS. Depending on the package used, additional input sections are needed.
CI
Configuration interaction (full CI, truncated CI, CAS-CI, etc) calculations are performed
by setting SCFTYP=NONE and CITYP=GUGA,ALDET,ORMAS. Each one of these packages
requires further input sections, which are typically slightly different from the input sections
needed for MCSCF runs.
GUGA: Unitary group CI package
The GUGA package is the only alternative if one wants CSFs with GAMESS. We subsequently provide a very brief description of the input sections needed to perform MCSCF, CASCI, truncated CI, and SOCI with this package. For a complete description of these methods and all the options available, please refer to the GAMESS input manual.
GUGA-MCSCF
The following input section performs a CASCI calculation with a CAS that includes 8 electrons in 8 orbitals (4 DOC and 4 VAL), for example, CAS(8,8). NMCC is the number of frozen orbitals (doubly occupied orbitals in all determinants), NDOC is the number of double occupied orbitals in the reference determinant, NVAL is the number of singly occupied orbitals in the reference (for spin polarized cases), and NVAL is the number of orbitals in the active space. Since FORS is set to .TRUE., all configurations in the active space will be included. ISTSYM defines the symmetry of the desired state.
$MCSCF CISTEP=GUGA MAXIT=1000 FULLNR=.TRUE. ACURCY=1.0D-5 $END
$DRT GROUP=C2v NMCC=0 NDOC=4 NALP=0 NVAL=4 ISTSYM=1 MXNINT= 500000 FORS=.TRUE. $END
GUGA-CASCI
The following input section performs a CASCI calculation with a CAS that includes 8 electrons in 8 orbitals (4 DOC and 4 VAL), for example, CAS(8,8). NFZC is the number of frozen orbitals (doubly occupied orbitals in all determinants). All other parameters are identical to those in the MCSCF input section.
$CIDRT GROUP=C2v NFZC=0 NDOC=4 NALP=0 NVAL=4 NPRT=2 ISTSYM=1 FORS=.TRUE. MXNINT= 500000 $END
$GUGDIA PRTTOL=0.001 CVGTOL=1.0E-5 ITERMX=1000 $END
GUGA-truncated CI
The following input sections will lead to a truncated CI calculation. In this particular case it will perform a CISD calculation since IEXCIT is set to 2. Other values in IEXCIT will lead to different CI truncations; for example, IEXCIT=4 will lead to CISDTQ. Notice that only the lowest 30 orbitals will be included in the generation of the excited determinants in this case. For a full CISD calculation, NVAL should be set to the total number of virtual orbitals.
$CIDRT GROUP=C2v NFZC=0 NDOC=4 NALP=0 NVAL=30 NPRT=2 ISTSYM=1 IEXCIT=2 MXNINT= 500000 $END
$GUGDIA PRTTOL=0.001 CVGTOL=1.0E-5 ITERMX=1000 $END
GUGA-SOCI
The following input section performs a SOCI calculation with a CAS that includes 8 electrons in 8 orbitals (4 DOC and 4 VAL), for example, CAS(8,8). Since SOCI is set to .TRUE., all single and double determinants from all determinants in the CAS(8,8) will be included.
$CIDRT GROUP=C2v NFZC=0 NDOC=4 NALP=0 NVAL=4 NPRT=2 ISTSYM=1 SOCI=.TRUE. NEXT=30 MXNINT= 500000 $END
$GUGDIA PRTTOL=0.001 CVGTOL=1.0E-5 ITERMX=1000 $END
ECP
To use ECPs in GAMESS, you must define a {$ECP ... $END}
block. There must be a definition of a potential for every atom in the system, including
symmetry equivalent ones. In addition, they must appear in the particular order expected
by GAMESS. The following example shows an ECP input block for a single water molecule using
BFD ECPs. To turn on the use of ECPs, the option “ECP=READ” must be added to the
CONTROL input block.
$ECP
O-QMC GEN 2 1
3
6.00000000 1 9.29793903
55.78763416 3 8.86492204
-38.81978498 2 8.62925665
1
38.41914135 2 8.71924452
H-QMC GEN 0 0
3
1.000000000000 1 25.000000000000
25.000000000000 3 10.821821902641
-8.228005709676 2 9.368618758833
H-QMC
$END
Appendix B: convert4qmc
To generate the particleset and wavefunction XML blocks required by QMCPACK in
calculations with molecular systems, the converter convert4qmc must be used. The converter
will read the standard output from the appropriate quantum chemistry calculation and will
generate all the necessary input for QMCPACK. In the following, we describe the main options of the
converter for GAMESS output. In general, there are three ways to use the converter depending
on the type of calculation performed. The minimum syntax for each option is shown subsequently.
For a description of the XML files produced by the converter, see Appendix E: Wavefunction XML block.
For all single-determinant calculations (HF and DFT with any DFTTYP):
convert4qmc -gamess single det.out
single det.out is the standard output generated by GAMESS.
(This option is not recommended. Use the following option to avoid mistakes.) For multideterminant calculations where the orbitals and configurations are read from different files (e.g., when using orbitals from a MCSCF run and configurations from a subsequent CI run):
convert4qmc -gamess orbitals multidet.out -ci cicoeff multidet.out
orbitals_multidet.out is the standard output from the calculation that generates the orbitals. cicoeff multidet.out is the standard output from the calculation that calculates the CI expansion.
For multideterminant calculations where the orbitals and configurations are read from the same file, using PRTMO=.T. in the GUESS input block:
convert4qmc -gamess multi det.out -ci multi det.out -readInitialGuess Norb
multi_det.out is the standard output from the calculation that calculates the CI expansion.
Options:
-gamess file.out: Standard output of GAMESS calculation. With the exception of determinant configurations and coefficients in multideterminant calculations, everything else is read from this file including atom coordinates, basis sets, SPOs, ECPs, number of electrons, multiplicity, etc.
-ci file.out: In multideterminant calculations, determinant configurations and coefficients are read from this file. Notice that SPOs are NOT read from this file. Recognized CI packages are ALDET, GUGA, and ORMAS. Output produced with the GUGA package MUST have the option “NPRT=2” in the CIDRT or DRT input blocks.
-threshold cutoff: Cutoff in multideterminant expansion. Only configurations with coefficients above this value are printed.
-zeroCI: Sets to zero the CI coefficients of all determinants, with the exception of the first one.
-readInitialGuess Norb: Reads Norb initial orbitals (“INITIAL GUESS ORBITALS”) from GAMESS output. These are orbitals generated by the GUESS input block and printed with the option “PRTMO=.T.”. Notice that this is useful only in combination with the option “GUESS=MOREAD” and in cases where the orbitals are not modified in the GAMESS calculation, e.g. CI runs. This is the recommended option in all CI calculations.
-NaturalOrbitals Norb: Read Norb “NATURAL ORBITALS” from GAMESS output. The natural orbitals must exists in the output, otherwise the code aborts.
-add3BodyJ: Adds 3-body Jastrow terms (e-e-I) between electron pairs (both same spin and opposite spin terms) and all ion species in the system. The radial function is initialized to zero, and the default cutoff is 10.0 bohr. The converter will add a 1- and 2-body Jastrow to the wavefunction block by default.
Useful notes
The type of SPOs read by the converter depends on the type of calculation and on the options used. By default, when neither -readInitialGuess nor -NaturalOrbitals are used, the following orbitals are read in each case (notice that -readInitialGuess or -NaturalOrbitals are mutually exclusive):
RHF and ROHF: “EIGENVECTORS”
MCSCF: “MCSCF OPTIMIZED ORBITALS”
GUGA, ALDET, ORMAS: Cannot read orbitals without -readInitialGuess or -NaturalOrbitals options.
The SPOs and printed CI coefficients in MCSCF calculations are not consistent in GAMESS. The printed CI coefficients correspond to the next-to-last iteration; they are not recalculated with the final orbitals. So to get appropriate CI coefficients from MCSCF calculations, a subsequent CI (no SCF) calculation is needed to produce consistent orbitals. In principle, it is possible to read the orbitals from the MCSCF output and the CI coefficients and configurations from the output of the following CI calculations. This could lead to problems in principle since GAMESS will rotate initial orbitals by default to obtain an initial guess consistent with the symmetry of the molecule. This last step is done by default and can change the orbitals reported in the MCSCF calculation before the CI is performed. To avoid this problem, we highly recommend using the preceding option #3 to read all the information from the output of the CI calculation; this requires the use of “PRTMO=.T.” in the GUESS input block. Since the orbitals are printed after any symmetry rotation, the resulting output will always be consistent.
Appendix C: Wavefunction optimization XML block
<loop max="10">
<qmc method="linear" move="pbyp" checkpoint="-1" gpu="no">
<parameter name="blocks"> 10 </parameter>
<parameter name="warmupsteps"> 25 </parameter>
<parameter name="steps"> 1 </parameter>
<parameter name="substeps"> 20 </parameter>
<parameter name="timestep"> 0.5 </parameter>
<parameter name="samples"> 10240 </parameter>
<cost name="energy"> 0.95 </cost>
<cost name="unreweightedvariance"> 0.0 </cost>
<cost name="reweightedvariance"> 0.05 </cost>
<parameter name="useDrift"> yes </parameter>
<parameter name="bigchange">10.0</parameter>
<estimator name="LocalEnergy" hdf5="no"/>
<parameter name="usebuffer"> yes </parameter>
<parameter name="MinMethod">quartic</parameter>
<parameter name="exp0">-6</parameter>
<parameter name="alloweddifference"> 1.0e-5 </parameter>
<parameter name="stepsize"> 0.15 </parameter>
<parameter name="nstabilizers"> 1 </parameter>
</qmc>
</loop>
Options:
bigchange: (default 50.0) Largest parameter change allowed
usebuffer: (default no) Save useful information during VMC
MinMethod: (default quartic) Method to calculate magnitude of parameter change quartic: fit quartic polynomial to four values of the cost function obtained using reweighting along chosen direction linemin: direct line minimization using reweighting rescale: no 1-D minimization. Uses Umrigars suggestions.
stepsize: (default 0.25) Step size in either quartic or linemin methods.
alloweddifference: (default 1e-4) Allowed increase in energy
exp0: (default -16.0) Initial value for stabilizer (shift to diagonal of H). Actual value of stabilizer is 10 exp0
nstabilizers: (default 3) Number of stabilizers to try
stabilizaterScale: (default 2.0) Increase in value of exp0 between iterations.
max its: (default 1) Number of inner loops with same sample
minwalkers: (default 0.3) Minimum value allowed for the ratio of effective samples to actual number of walkers in a reweighting step. The optimization will stop if the effective number of walkers in any reweighting calculation drops below this value. Last set of acceptable parameters are kept.
maxWeight: (defaul 1e6) Maximum weight allowed in reweighting. Any weight above this value will be reset to this value.
Recommendations:
Set samples to equal to (#threads)*blocks.
Set steps to 1. Use substeps to control correlation between samples.
For cases where equilibration is slow, increase both substeps and warmupsteps.
For hard cases (e.g., simultaneous optimization of long MSD and 3-Body J), set exp0 to 0 and do a single inner iteration (max its=1) per sample of configurations.
Appendix D: VMC and DMC XML block
<qmc method="vmc" move="pbyp" checkpoint="-1">
<parameter name="useDrift">yes</parameter>
<parameter name="warmupsteps">100</parameter>
<parameter name="blocks">100</parameter>
<parameter name="steps">1</parameter>
<parameter name="substeps">20</parameter>
<parameter name="walkers">30</parameter>
<parameter name="timestep">0.3</parameter>
<estimator name="LocalEnergy" hdf5="no"/>
</qmc>
<qmc method="dmc" move="pbyp" checkpoint="-1">
<parameter name="nonlocalmoves">yes</parameter>
<parameter name="targetWalkers">1920</parameter>
<parameter name="blocks">100</parameter>
<parameter name="steps">100</parameter>
<parameter name="timestep">0.1</parameter>
<estimator name="LocalEnergy" hdf5="no"/>
</qmc>
General Options:
move: (default “walker”) Type of electron move. Options: “pbyp” and “walker.”
checkpoint: (default “-1”) (If > 0) Generate checkpoint files with given frequency. The calculations can be restarted/continued with the produced checkpoint files.
useDrift: (default “yes”) Defines the sampling mode. useDrift = “yes” will use Langevin acceleration to sample the VMC and DMC distributions, while useDrift=“no” will use random displacements in a box.
warmupSteps: (default 0) Number of steps warmup steps at the beginning of the calculation. No output is produced for these steps.
blocks: (default 1) Number of blocks (outer loop).
steps: (default 1) Number of steps per blocks (middle loop).
sub steps: (default 1) Number of substeps per step (inner loop). During substeps, the local energy is not evaluated in VMC calculations, which leads to faster execution. In VMC calculations, set substeps to the average autocorrelation time of the desired quantity.
time step: (default 0.1) Electronic time step in bohr.
samples: (default 0) Number of walker configurations saved during the current calculation.
walkers: (default #threads) In VMC, sets the number of walkers per node. The total number of walkers in the calculation will be equal to walkers*(# nodes).
Options unique to DMC:
targetWalkers: (default #walkers from previous calculation, e.g., VMC). Sets the target number of walkers. The actual population of walkers will fluctuate around this value. The walkers will be distributed across all the nodes in the calculation. On a given node, the walkers are split across all the threads in the system.
nonlocalmoves: (default “no”) Set to “yes” to turns on the use of Casula’s T-moves.
Appendix E: Wavefunction XML block
<wavefunction name="psi0" target="e">
<determinantset type="MolecularOrbital" name="LCAOBSet"
source="ion0" transform="yes">
<basisset name="LCAOBSet">
<atomicBasisSet name="Gaussian-G2" angular="cartesian" type="Gaussian" elementType="O" normalized="no">
...
</atomicBasisSet>
</basisset>
<slaterdeterminant>
<determinant id="updet" size="4">
<occupation mode="ground"/>
<coefficient size="57" id="updetC">
...
</coefficient>
</determinant>
<determinant id="downdet" size="4">
<occupation mode="ground"/>
<coefficient size="57" id="downdetC">
...
</coefficient>
</determinant>
</slaterdeterminant>
</determinantset>
<jastrow name="J2" type="Two-Body" function="Bspline" print="yes">
...
</jastrow>
</wavefunction>
In this section we describe the basic format of a QMCPACK wavefunction XML block. Everything listed in this section is generated by the appropriate converter tools. Little to no modification is needed when performing standard QMC calculations. As a result, this section is meant mainly for illustration purposes. Only experts should attempt to modify these files (with very few exceptions like the cutoff of CI coefficients and the cutoff in Jastrow functions) since changes can lead to unexpected results.
A QMCPACK wavefunction XML block is a combination of a determinantset, which contains the antisymmetric part of the wavefunction and one or more Jastrow blocks. The syntax of the antisymmetric block depends on whether the wavefunction is a single determinant or a multideterminant expansion. Listing 62 shows the general structure of the single-determinant case. The determinantset block is composed of a basisset block, which defines the atomic orbital basis set, and a slaterdeterminant block, which defines the SPOs and occupation numbers of the Slater determinant. Listing 63 shows a (piece of a) sample of a slaterdeterminant block. The slaterdeterminant block consists of two determinant blocks, one for each electron spin. The parameter “size” in the determinant block refers to the number of SPOs present while the “size” parameter in the coefficient block refers to the number of atomic basis functions per SPO.
<slaterdeterminant>
<determinant id="updet" size="5">
<occupation mode="ground"/>
<coefficient size="134" id="updetC">
9.55471000000000e-01 -3.87000000000000e-04 6.51140000000000e-02 2.17700000000000e-03
1.43900000000000e-03 4.00000000000000e-06 -4.58000000000000e-04 -5.20000000000000e-05
-2.40000000000000e-05 6.00000000000000e-06 -0.00000000000000e+00 -0.00000000000000e+00
-0.00000000000000e+00 -0.00000000000000e+00 -0.00000000000000e+00 -0.00000000000000e+00
-0.00000000000000e+00 -0.00000000000000e+00 -0.00000000000000e+00 -0.00000000000000e+00
-0.00000000000000e+00 -0.00000000000000e+00 -0.00000000000000e+00 -0.00000000000000e+00
-0.00000000000000e+00 -0.00000000000000e+00 -0.00000000000000e+00 -0.00000000000000e+00
-0.00000000000000e+00 -0.00000000000000e+00 -0.00000000000000e+00 -0.00000000000000e+00
-0.00000000000000e+00 -0.00000000000000e+00 -0.00000000000000e+00 -0.00000000000000e+00
-0.00000000000000e+00 -5.26000000000000e-04 2.63000000000000e-04 2.63000000000000e-04
-0.00000000000000e+00 -0.00000000000000e+00 -0.00000000000000e+00 -1.27000000000000e-04
6.30000000000000e-05 6.30000000000000e-05 -0.00000000000000e+00 -0.00000000000000e+00
-0.00000000000000e+00 -3.20000000000000e-05 1.60000000000000e-05 1.60000000000000e-05
-0.00000000000000e+00 -0.00000000000000e+00 -0.00000000000000e+00 7.00000000000000e-06
Listing 64 shows the general structure of the multideterminant case. Similar to the single-determinant case, the determinantset must contain a basisset block. This definition is identical to the one described previously. In this case, the definition of the SPOs must be done independently from the definition of the determinant configurations; the latter is done in the sposet block, while the former is done on the multideterminant block. Notice that two sposet sets must be defined, one for each electron spin. The name of each sposet set is required in the definition of the multideterminant block. The determinants are defined in terms of occupation numbers based on these orbitals.
<wavefunction id="psi0" target="e">
<determinantset name="LCAOBSet" type="MolecularOrbital" transform="yes" source="ion0">
<basisset name="LCAOBSet">
<atomicBasisSet name="Gaussian-G2" angular="cartesian" type="Gaussian" elementType="O" normalized="no">
...
</atomicBasisSet>
...
</basisset>
<sposet basisset="LCAOBSet" name="spo-up" size="8">
<occupation mode="ground"/>
<coefficient size="40" id="updetC">
...
</coefficient>
</sposet>
<sposet basisset="LCAOBSet" name="spo-dn" size="8">
<occupation mode="ground"/>
<coefficient size="40" id="downdetC">
...
</coefficient>
</sposet>
<multideterminant optimize="yes" spo_up="spo-up" spo_dn="spo-dn">
<detlist size="97" type="CSF" nca="0" ncb="0" nea="4" neb="4" nstates="8" cutoff="0.001">
<csf id="CSFcoeff_0" exctLvl="0" coeff="0.984378" qchem_coeff="0.984378" occ="22220000">
<det id="csf_0-0" coeff="1" alpha="11110000" beta="11110000"/>
</csf>
...
</detlist>
</multideterminant>
</determinantset>
<jastrow name="J2" type="Two-Body" function="Bspline" print="yes">
...
</jastrow>
</wavefunction>
There are various options in the multideterminant block that users should be aware of.
cutoff: (IMPORTANT! ) Only configurations with (absolute value) “qchem coeff” larger than this value will be read by QMCPACK.
optimize: Turn on/off the optimization of linear CI coefficients.
coeff: (in csf ) Current coefficient of given configuration. Gets updated during wavefunction optimization.
qchem coeff: (in csf ) Original coefficient of given configuration from GAMESS calculation. This is used when applying a cutoff to the configurations read from the file. The cutoff is applied on this parameter and not on the optimized coefficient.
nca and nab: Number of core orbitals for up/down electrons. A core orbital is an orbital that is doubly occupied in all determinant configurations, not to be confused with core electrons. These are not explicitly listed on the definition of configurations.
nea and neb: Number of up/down active electrons (those being explicitly correlated).
nstates: Number of correlated orbitals.
size (in detlist ): Contains the number of configurations in the list.
The remaining part of the determinantset block is the definition of Jastrow factor. Any
number of these can be defined. Listing 65 shows a sample Jastrow
block including 1-, 2- and 3-body terms. This is the standard block produced by
convert4qmc with the option -add3BodyJ (this particular example is for a water molecule).
Optimization of individual radial functions can be turned on/off using the “optimize”
parameter. It can be added to any coefficients block, even though it is currently not
present in the J1 and J2 blocks.
<jastrow name="J2" type="Two-Body" function="Bspline" print="yes">
<correlation rcut="10" size="10" speciesA="u" speciesB="u">
<coefficients id="uu" type="Array">0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0</coefficients>
</correlation>
<correlation rcut="10" size="10" speciesA="u" speciesB="d">
<coefficients id="ud" type="Array">0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0</coefficients>
</correlation>
</jastrow>
<jastrow name="J1" type="One-Body" function="Bspline" source="ion0" print="yes">
<correlation rcut="10" size="10" cusp="0" elementType="O">
<coefficients id="eO" type="Array">0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0</coefficients>
</correlation>
<correlation rcut="10" size="10" cusp="0" elementType="H">
<coefficients id="eH" type="Array">0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0</coefficients>
</correlation>
</jastrow>
<jastrow name="J3" type="eeI" function="polynomial" source="ion0" print="yes">
<correlation ispecies="O" especies="u" isize="3" esize="3" rcut="10">
<coefficients id="uuO" type="Array" optimize="yes">
</coefficients>
</correlation>
<correlation ispecies="O" especies1="u" especies2="d" isize="3" esize="3" rcut="10">
<coefficients id="udO" type="Array" optimize="yes">
</coefficients>
</correlation>
<correlation ispecies="H" especies="u" isize="3" esize="3" rcut="10">
<coefficients id="uuH" type="Array" optimize="yes">
</coefficients>
</correlation>
<correlation ispecies="H" especies1="u" especies2="d" isize="3" esize="3" rcut="10">
<coefficients id="udH" type="Array" optimize="yes">
</coefficients>
</correlation>
</jastrow>
This training assumes basic familiarity with the UNIX operating system. In particular, we use simple scripts written in “csh.” In addition, we assume you have obtained all the necessary files and executables and that the training files are located at ${TRAINING TOP}.
The goal of this training is not only to familiarize you with the execution and options in QMCPACK but also to introduce you to important concepts in QMC calculations and many-body electronic structure calculations.