Trial wavefunction specification

Introduction

This section describes the input blocks associated with the specification of the trial wavefunction in a QMCPACK calculation. These sections are contained within the <wavefunction> \(...\) </wavefunction> xml blocks. Users are expected to rely on converters to generate the input blocks described in this section. The converters and the workflows are designed such that input blocks require minimum modifications from users. Unless the workflow requires modification of wavefunction blocks (e.g., setting the cutoff in a multideterminant calculation), only expert users should directly alter them.

The trial wavefunction in QMCPACK has a general product form:

(1)\[\Psi_T(\vec{r}) = \prod_k \Theta_k(\vec{r}) ,\]

where each \(\Theta_k(\vec{r})\) is a function of the electron coordinates (and possibly ionic coordinates and variational parameters). For problems involving electrons, the overall trial wavefunction must be antisymmetric with respect to electron exchange, so at least one of the functions in the product must be antisymmetric. Notice that, although QMCPACK allows for the construction of arbitrary trial wavefunctions based on the functions implemented in the code (e.g., slater determinants, jastrow functions), the user must make sure that a correct wavefunction is used for the problem at hand. From here on, we assume a standard trial wavefunction for an electronic structure problem

(2)\[Psi_T(\vec{r}) = \textit{A}(\vec{r}) \prod_k \textit{J}_k(\vec{r}),\]

where \(\textit{A}(\vec{r})\) is one of the antisymmetric functions: (1) slater determinant, (2) multislater determinant, or (3) pfaffian and \(\textit{J}_k\) is any of the Jastrow functions (described in Jastrow Factors). The antisymmetric functions are built from a set of single particle orbitals (SPO) (sposet). QMCPACK implements four different types of sposet, described in the following section. Each sposet is designed for a different type of calculation, so their definition and generation varies accordingly.

Listing 1 wavefunction XML element skeleton.

<wavefunction>
  <sposet_collection ...>
    <sposet ...>
      ...
    </sposet>
  </sposet_collection>
  <determinantset>
    <slaterdeterminant ...>
      ...
    </slaterdeterminant>
    <backflow>
      ...
    </backflow>
  </determinantset>
  <jastrow ...>
  </jastrow>
</wavefunction>

Single-particle orbitals

A single particle orbital set (SPOSet) is a set of orbitals evaluated at a single electron real-space position. A typical Slater determinant is calculated from a N-by-N matrix constructed from N orbitals at the positions of N electrons. QMCPACK supports a range of SPOSet types: * 3D B-splines orbitals * Linear combination of atomic orbitals (LCAO) with Gaussian and/or Slater-type basis sets * Hybrid orbital representation * Plane-wave basis sets

sposet_collection input style

Listing 2 SPO XML element framework.

<!-- build a sposet collection of type bspline. /-->
<sposet_collection type="bspline" ...>
  <sposet name="spo-up" ... /sposet>
  ...
</sposet_collection>

The sposet_collection element forms the container for sposet and a few other tags. The contents and attributes in a sposet_collection node and sposet node depend on the type being used. The name of each sposet must be unique. It is used for look-up by Single determinant wavefunctions and Multideterminant wavefunctions.

sposet_collection element:

Parent elements	wavefunction
Child elements	sposet

attribute:

Name	Datatype	Values	Default	Description
type	Text	See below	‘’ ‘’	Type of sposet

type Type of sposet. Accepted values are ‘spline’ (‘bspline’ or ‘einspline’), ‘MolecularOrbital’, ‘pw’, ‘heg’, ‘composite’.

If QMCPACK printout contains !!!!!!! Deprecated input style: creating SPO set inside determinantset. Support for this usage will soon be removed. SPO sets should be built outside., users need to update the input XML by moving all the SPOSet construction related details out of determinantset. This revised specification keeps the basis set details separate from information about the determinants.

Listing 3 Deprecated input style.

<determinantset type="einspline" href="pwscf.pwscf.h5" tilematrix="2 0 0 0 1 0 0 0 1" source="ion0" meshfactor="1.0" precision="double">
   <slaterdeterminant>
      <determinant id="updet" size="8">
         <occupation mode="ground" spindataset="0"/>
      </determinant>
      <determinant id="downdet" size="8">
         <occupation mode="ground" spindataset="0"/>
      </determinant>
   </slaterdeterminant>
</determinantset>

After updating the input style.

Listing 4 Updated input style.

<!-- all the attributes are moved from determinantset.-->
<sposet_collection type="einspline" href="pwscf.pwscf.h5" tilematrix="2 0 0 0 1 0 0 0 1" source="ion0" meshfactor="1.0" precision="double">
  <!-- all the attributes and contents are moved from determinant.  Change 'id' tag to 'name' tag.
       Need only one sposet for unpolarized calculation.-->
  <sposet name="spo-ud" size="8">
     <occupation mode="ground" spindataset="0"/>
  </sposet>
</sposet_collection>
<determinantset>
   <slaterdeterminant>
      <!-- build two determinants from the same sposet named 'spo-ud'. One for each spin.-->
      <determinant sposet="spo-ud"/>
      <determinant sposet="spo-ud"/>
   </slaterdeterminant>
</determinantset>

In the case of multi-determinants, all the attributes of determinantset need to be moved to sposet_collection and existing sposet xml nodes need to be moved under sposet_collection. If there is a basisset node, it needs to be moved under sposet_collection as well.

3D B-splines orbitals

In this section we describe the use of spline basis sets to expand the sposet. Spline basis sets are designed to work seamlessly with plane wave DFT codes (e.g.,Quantum ESPRESSO as a trial wavefunction generator). Codes that utilize regular real space grids as a basis can also be seamlessly interfaced.

In QMC algorithms, all the SPOs \(\{\phi(\vec{r})\}\) need to be updated every time a single electron moves. Evaluating SPOs takes a very large portion of computation time. In principle, PW basis set can be used to express SPOs directly in QMC, as in DFT. But it introduces an unfavorable scaling because the basis set size increases linearly as the system size. For this reason, it is efficient to use a localized basis with compact support and a good transferability from the plane wave basis.

In particular, 3D tricubic B-splines provide a basis in which only 64 elements are nonzero at any given point in [AlfeG04]. The 1D cubic B-spline is given by

(3)\[f(x) = \sum_{i'=i-1}^{i+2} b^{i'\!,3}(x)\,\, p_{i'},\]

where \(b^{i}(x)\) is the piecewise cubic polynomial basis functions and \(i = \text{floor}(\Delta^{-1} x)\) is the index of the first grid point \(\le x\). Constructing a tensor product in each Cartesian direction, we can represent a 3D orbital as

(4)\[\phi_n(x,y,z) = \!\!\!\!\sum_{i'=i-1}^{i+2} \!\! b_x^{i'\!,3}(x) \!\!\!\!\sum_{j'=j-1}^{j+2} \!\! b_y^{j'\!,3}(y) \!\!\!\!\sum_{k'=k-1}^{k+2} \!\! b_z^{k'\!,3}(z) \,\, p_{i', j', k',n}.\]

This allows the rapid evaluation of each orbital in constant time unlike with a plane wave basis set where the cost increases with system size. Furthermore, this basis is systematically improvable with a single spacing parameter so that accuracy is not compromised compared with the plane wave basis.

The use of 3D tricubic B-splines greatly improves computational efficiency. The gain in computation time compared to an equivalent plane wave basis set becomes increasingly large as the system size grows. On the downside, this computational efficiency comes at the expense of increased memory use, which is easily overcome, however, by the large aggregate memory available per node through OpenMP/MPI hybrid QMC.

The input xml block for the spline SPOs is given in Spline SPO XML element. A list of options is given in table3.

Listing 5 Spline SPO XML element

<sposet_collection type="bspline" source="i" href="pwscf.h5"
                tilematrix="1 1 3 1 2 -1 -2 1 0" gpu="yes" meshfactor="0.8"
                twist="0  0  0" precision="double">
  <sposet name="spo-up" size="208">
    <occupation mode="ground" spindataset="0"/>
  </sposet>
  <!-- spin polarized case needs two sposets /-->
  <sposet name="spo-dn" size="208">
    <occupation mode="ground" spindataset="1"/>
  </sposet>
</sposet_collection>

sposet_collection element:

Parent elements	wavefunction
Child elements	sposet

attribute:

Name	Datatype	Values	Default	Description
type	Text	Bspline		Type of sposet
href	Text			Path to hdf5 file from pw2qmcpack.x.
tilematrix	9 integers			Tiling matrix used to expand supercell.
twistnum	Integer			Index of the super twist.
twist	3 floats			Super twist.
meshfactor	Float	\(\le 1.0\)		Grid spacing ratio.
precision	Text	Single/double		Precision of spline coefficients
gpu	Text	Yes/no		GPU switch.
check_orb_norm	Text	Yes/no	Yes	Check norms of orbitals from h5 file.
save_coefs	Text	Yes/no	No	Save the spline coefficients to h5 file.
source	Text	Any	Ion0	Particle set with atomic positions.
skip_checks	Text	Yes/no	No	skips checks for ion information in h5

Table 3 Options for the sposet_collection xml-block associated with B-spline single particle orbital sets.

Additional information:

• precision

  Only effective on CPU versions without mixed precision, “single” is always imposed with mixed precision. Using single precision not only saves memory use but also speeds up the B-spline evaluation. We recommend using single precision since we saw little chance of really compromising the accuracy of calculation.

• meshfactor

  The ratio of actual grid spacing of B-splines used in QMC calculation with respect to the original one calculated from h5. A smaller meshfactor saves memory use but reduces accuracy. The effects are similar to reducing plane wave cutoff in DFT calculations. Use with caution!

• twistnum

  We recommend not using it in the input because the ordering of orbitals depends on how they are being stored in the h5 file. twistnum gets ignored if twist exists in the input. If positive, it is the index. If negative, the super twist is referred by twist. This input parameter is kept only for keeping old input files working.

• twist

  The twist angle. If neither twist nor twistnum is provided, Take Gamma point, (0, 0, 0).

• save_coefs

  If yes, dump the real-space B-spline coefficient table into an h5 file on the disk. When the orbital transformation from k space to B-spline requires more than the available amount of scratch memory on the compute nodes, users can perform this step on fat nodes and transfer back the h5 file for QMC calculations.

• skip_checks

  When converting the wave function from convertpw4qmc instead of pw2qmcpack, there is missing ionic information. This flag bypasses the requirement that the ionic information in the eshdf.h5 file match the input xml.

Linear combination of atomic orbitals (LCAO) with Gaussian and/or Slater-type basis sets

In this section we describe the use of localized basis sets to expand the sposet. The general form of a single particle orbital in this case is given by:

(5)\[\phi_i(\vec{r}) = \sum_k C_{i,k} \ \eta_k(\vec{r}),\]

where \(\{\eta_k(\vec{r})\}\) is a set of M atom-centered basis functions and \(C_{i,k}\) is a coefficient matrix. This should be used in calculations of finite systems employing an atom-centered basis set and is typically generated by the convert4qmc converter. Examples include calculations of molecules using Gaussian basis sets or Slater-type basis functions. Initial support for periodic systems is described in Periodic LCAO for Solids. Even though this section is called “Gaussian basis sets” (by far the most common atom-centered basis set), QMCPACK works with any atom-centered basis set based on either spherical harmonic angular functions or Cartesian angular expansions. The radial functions in the basis set can be expanded in either Gaussian functions, Slater-type functions, or numerical radial functions.

In this section we describe the input sections of sposet_collection for the atom-centered basis set. Here is an example of single determinant with LCAO. The input sections for multideterminant trial wavefunctions are described in Multideterminant wavefunctions.

Listing 6 slaterdeterminant with an LCAO sposet_collection example

<sposet_collection type="MolecularOrbital" source="ion0" cuspCorrection="no">
  <basisset name="LCAOBSet">
    <atomicBasisSet name="Gaussian-G2" angular="cartesian" elementType="H" normalized="no">
      <grid type="log" ri="1.e-6" rf="1.e2" npts="1001"/>
      <basisGroup rid="H00" n="0" l="0" type="Gaussian">
        <radfunc exponent="5.134400000000e-02" contraction="1.399098787100e-02"/>
      </basisGroup>
    </atomicBasisSet>
  </basisset>
  <sposet name="spo" basisset="LCAOBSet" size="1">
    <occupation mode="ground"/>
    <coefficient size="1" id="updetC">
      1.00000000000000e+00
    </coefficient>
  </sposet>
</sposet_collection>
<determinantset>
   <slaterdeterminant>
      <determinant sposet="spo" />
   </slaterdeterminant>
</determinantset>

Here is the basic structure for LCAO sposet_collection input block. A list of options for sposet_collection is given in table4.

Listing 7 Basic input block for sposet_collection for LCAO.

<sposet_collection type="MolecularOrbital" ...>
  <basisset name="LCAOBSet" ...>
    ...
  </basisset>
  <sposet name="spo" basisset="LCAOBSet" size="1">
    <occupation mode="ground"/>
    <coefficient size="1" id="updetC">
      1.00000000000000e+00
    </coefficient>
  </sposet>
</sposet_collection>

The definition of the set of atom-centered basis functions is given by the basisset block and the sposet defined within sposet_collection. The basisset input block is composed from a collection of atomicBasisSet input blocks, one for each atomic species in the simulation where basis functions are centered. The general structure for basisset and atomicBasisSet are given in Listing 4, and the corresponding lists of options are given in table5 and table6.

sposet_collection element:

Parent elements	wavefunction
Child elements	basisset , sposet

Attribute:

Name	Datatype	Values	Default	Description
name/id	Text	Any	‘’ ‘’	Name of determinant set
type	Text	See below	‘’ ‘’	Type of sposet
keyword	Text	NMO, GTO, STO	NMO	Type of orbital set generated
transform	Text	Yes/no	Yes	Transform to numerical radial functions?
source	Text	Any	Ion0	Particle set with the position of atom centers
cuspCorrection	Text	Yes/no	No	Apply cusp correction scheme to sposet?

Table 4 Options for the sposet_collection xml-block associated with atom-centered single particle orbital sets.

• type

  Type of sposet. For atom-centered based sposets, use type=”MolecularOrbital” or type=”MO”.

• keyword/key

  Type of basis set generated, which does not necessarily match the type of basis set on the input block. The three possible options are: NMO (numerical molecular orbitals), GTO (Gaussian-type orbitals), and STO (Slater-type orbitals). The default option is NMO. By default, QMCPACK will generate numerical orbitals from both GTO and STO types and use cubic or quintic spline interpolation to evaluate the radial functions. This is typically more efficient than evaluating the radial functions in the native basis (Gaussians or exponents) and allows for arbitrarily large contractions without any additional cost. To force use of the native expansion (not recommended), use GTO or STO for each type of input basis set.

• transform

  Request (or avoid) a transformation of the radial functions to NMO type. The default and recommended behavior is to transform to numerical radial functions. If transform is set to yes, the option keyword is ignored.

• cuspCorrection

  Enable (disable) use of the cusp correction algorithm (CASINO REFERENCE) for a basisset built with GTO functions. The algorithm is implemented as described in (CASINO REFERENCE) and works only with transform=”yes” and an input GTO basis set. No further input is needed.

Listing 8 Basic input block for basisset.

<basisset name="LCAOBSet">
  <atomicBasisSet name="Gaussian-G2" angular="cartesian" elementType="C" normalized="no">
    <grid type="log" ri="1.e-6" rf="1.e2" npts="1001"/>
    <basisGroup rid="C00" n="0" l="0" type="Gaussian">
      <radfunc exponent="5.134400000000e-02" contraction="1.399098787100e-02"/>
      ...
    </basisGroup>
    ...
  </atomicBasisSet>
  <atomicBasisSet name="Gaussian-G2" angular="cartesian" type="Gaussian" elementType="C" normalized="no">
    ...
  </atomicBasisSet>
  ...
</basisset>

basisset element:

Parent elements	sposet_collection
Child elements	atomicBasisSet

Attribute:

Name	Datatype	Values	Default	Description
name / id	Text	Any	” “	Name of atom-centered basis set

Table 5 Options for the basisset xml-block associated with atom-centered single particle orbital sets.

AtomicBasisSet element:

Parent elements	basisset
Child elements	grid , basisGroup

Attribute:

Name	Datatype	Values	Default	Description
name / id	Text	Any	” “	Name of atomic basis set
angular	Text	See below	Default	Type of angular functions
expandYlm	Text	See below	Yes	Expand Ylm shells?
expM	Text	See below	Yes	Add sign for \((-1)^{m}\)?
elementType/species	Text	Any	e	Atomic species where functions are centered
normalized	Text	Yes/no	Yes	Are single particle functions normalized?

Table 6 Options for the atomicBasisSet xml-block.

• name/id

  Name of the basis set. Names should be unique.

• angular

  Type of angular functions used in the expansion. In general, two angular basis functions are allowed: “spherical” (for spherical Ylm functions) and “Cartesian” (for functions of the type \(x^{n}y^{m}z^{l}\)).

• expandYlm

  Determines whether each basis group is expanded across the corresponding shell of m values (for spherical type) or consistent powers (for Cartesian functions). Options:

  • “No”: Do not expand angular functions across corresponding angular shell.

  • “Gaussian”: Expand according to Gaussian03 format. This function is compatible only with angular=”spherical.” For a given input (l,m), the resulting order of the angular functions becomes (1,-1,0) for l=1 and (0,1,-1,2,-2,…,l,-l) for general l.

  • “Natural”: Expand angular functions according to (-l,-l+1,…,l-1,l).

  • “Gamess”: Expand according to Gamess’ format for Cartesian functions. Notice that this option is compatible only with angular=”Cartesian.” If angular=”Cartesian” is used, this option is not necessary.

• expM

  Determines whether the sign of the spherical Ylm function associated with m (\(-1^{m}\)) is included in the coefficient matrix or not.

• elementType/species

  Name of the species where basis functions are centered. Only one atomicBasisSet block is allowed per species. Additional blocks are ignored. The corresponding species must exist in the particleset given as the source option to determinantset. Basis functions for all the atoms of the corresponding species are included in the basis set, based on the order of atoms in the particleset.

basicGroup element:

Parent elements	AtomicBasisSet
Child elements	radfunc

Attribute:

Name	Datatype	Values	Default	Description
rid/id	Text	Any	‘’ ‘’	Name of the basisGroup
type	Text	Any	‘’ ‘’	Type of basisGroup
n/l/m/s	Integer	Any	0	Quantum numbers of basisGroup

table7 Options for the basisGroup xml-block.

• type

  Type of input basis radial function. Note that this refers to the type of radial function in the input xml-block, which might not match the radial function generated internally and used in the calculation (if transform is set to “yes”). Also note that different basisGroup blocks within a given atomicBasisSet can have different types.

• n/l/m/s

  Quantum numbers of the basis function. Note that if expandYlm is set to “yes” in atomicBasisSet, a full shell of basis functions with the appropriate values of “m” will be defined for the corresponding value of “l.” Otherwise a single basis function will be given for the specific combination of “(l,m).”

radfunc element:

attributes for type = “Gaussian”:

TBDoc

Hybrid orbital representation

The hybrid representation of the single particle orbitals combines a localized atomic basis set around atomic cores and B-splines in the interstitial regions to reduce memory use while retaining high evaluation speed and either retaining or increasing overall accuracy. Full details are provided in [LEKS18], and users of this feature are kindly requested to cite this paper. In practice, we have seen that using a meshfactor=0.5 is often possible and achieves huge memory savings. Fig. 3 illustrates how the regions are assigned.

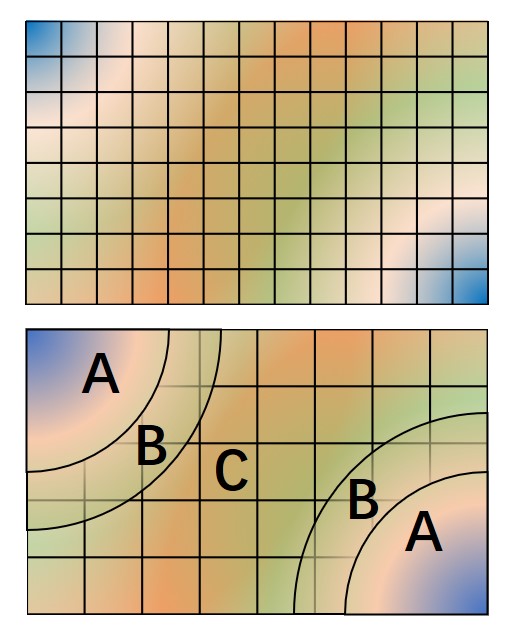
Fig. 3 Regular and hybrid orbital representation. Regular B-spline representation (left panel) contains only one region and a sufficiently fine mesh to resolve orbitals near the nucleus. The hybrid orbital representation (right panel) contains near nucleus regions (A) where spherical harmonics and radial functions are used, buffers or interpolation regions (B), and an interstitial region (C) where a coarse B-spline mesh is used.

Orbitals within region A are computed as

\[\phi^A_n({\bf r})=R_{n,l,m}(r)Y_{l,m}(\hat{r})\]

Orbitals in region C are computed as the regular B-spline basis described in 3D B-splines orbitals above. The region B interpolates between A and C as

(6)\[\phi^B_n({\bf r}) = S(r) \phi^A_n({\bf r}) + (1-S(r))\phi^C_n({\bf r})\]

(7)\[(S(r) = \frac{1}{2}-\frac{1}{2} tanh \left[\alpha\left(\frac{r-r_{\rm A/B}}{r_{\rm B/C}-r_{\rm A/B}}-\frac{1}{2}\right)\right]\]

To enable hybrid orbital representation, the input XML needs to see the tag hybridrep="yes" shown in Listing 6.

Listing 9 Hybrid orbital representation input example.

<sposet_collection type="bspline" source="i" href="pwscf.h5"
              tilematrix="1 1 3 1 2 -1 -2 1 0" gpu="yes" meshfactor="0.8"
              twist="0  0  0" precision="single" hybridrep="yes">
  ...
</sposet_collection>

Second, the information describing the atomic regions is required in the particle set, shown in Listing 7.

Listing 10 particleset elements for ions with information needed by hybrid orbital representation.

<group name="Ni">
  <parameter name="charge">          18 </parameter>
  <parameter name="valence">         18 </parameter>
  <parameter name="atomicnumber" >   28 </parameter>
  <parameter name="cutoff_radius" > 1.6 </parameter>
  <parameter name="inner_cutoff" >  1.3 </parameter>
  <parameter name="lmax" >            5 </parameter>
  <parameter name="spline_radius" > 1.8 </parameter>
  <parameter name="spline_npoints">  91 </parameter>
</group>

The parameters specific to hybrid representation are listed as

attrib element

Attribute:

Name	Datatype	Values	Default	Description
cutoff_radius	Real	>=0.0	None	Cutoff radius for B/C boundary
lmax	Integer	>=0	None	Largest angular channel
inner_cutoff	Real	>=0.0	Dep.	Cutoff radius for A/B boundary
spline_radius	Real	>0.0	Dep.	Radial function radius used in spine
spline_npoints	Integer	>0	Dep.	Number of spline knots

• cutoff_radius is required for every species. If a species is intended to not be covered by atomic regions, setting the value 0.0 will put default values for all the reset parameters. A good value is usually a bit larger than the core radius listed in the pseudopotential file. After a parametric scan, pick the one from the flat energy region with the smallest variance.

• lmax is required if cutoff_radius \(>\) 0.0. This value usually needs to be at least the highest angular momentum plus 2.

• inner_cutoff is optional and set as cutoff_radius \(-0.3\) by default, which is fine in most cases.

• spline_radius and spline_npoints are optional. By default, they are calculated based on cutoff_radius and a grid displacement 0.02 bohr. If users prefer inputing them, it is required that cutoff_radius <= spline_radius \(-\) 2 \(\times\) spline_radius/(spline_npoints \(-\) 1).

In addition, the hybrid orbital representation allows extra optimization to speed up the nonlocal pseudopotential evaluation using the batched algorithm listed in Pseudopotentials.

Plane-wave basis sets

Homogeneous electron gas

The interacting Fermi liquid can be created using a determinant of free-particle orbitals. The lowest-energy plane-wave states compatible with the boundary condition are occupied.

This following example can also be used for Helium simulations by specifying the proper pair interaction in the Hamiltonian section and using a bosonic wavefunction.

Listing 11 2D Fermi liquid example: particle specification

<simulationcell name="global">
  <parameter name="rs" pol="0" condition="74">6.5</parameter>
  <parameter name="bconds">p p p</parameter>
  <parameter name="LR_dim_cutoff">15</parameter>
</simulationcell>
<particleset name="e" random="yes">
  <group name="u" size="37">
    <parameter name="charge">-1</parameter>
    <parameter name="mass">1</parameter>
  </group>
  <group name="d" size="37">
    <parameter name="charge">-1</parameter>
    <parameter name="mass">1</parameter>
  </group>
</particleset>

Listing 12 2D Fermi liquid example (Slater Jastrow wavefunction)

<wavefunction name="psi0" target="e">
<sposet_builder type="free">
  <sposet name="spo-ud" size="37" twist="0 0 0"/>
</sposet_builder>
<determinantset>
  <slaterdeterminant>
    <determinant id="updet" sposet="spo-ud"/>
    <determinant id="dndet" sposet="spo-ud"/>
  </slaterdeterminant>
</determinantset>
<jastrow name="J2" type="Two-Body" function="Bspline" print="no">
  <correlation speciesA="u" speciesB="u" size="8" cusp="0">
    <coefficients id="uu" type="Array" optimize="yes">
  </correlation>
  <correlation speciesA="u" speciesB="d" size="8" cusp="0">
    <coefficients id="ud" type="Array" optimize="yes">
  </correlation>
</jastrow>
</wavefunction>

Single determinant wavefunctions

Placing a single determinant for each spin is the most used ansatz for the antisymmetric part of a trial wavefunction. The input xml block for slaterdeterminant is given in Listing 1. A list of options is given in Table2.

slaterdeterminant element:

Parent elements	determinantset
Child elements	determinant

Attribute:

Name	Datatype	Values	Default	Description
delay_rank	Integer	>=0	1	Number of delayed updates.
optimize	Text	yes/no	yes	Enable orbital optimization.
gpu	Text	yes/no	yes	Use the GPU acceleration implementation.
batch	Text	yes/no	dep.	Select the batched walker implementation.
matrix_inverter	Text	gpu/host	gpu	Slater matrix inversion scheme.

Table 2 Options for the slaterdeterminant xml-block.

Listing 13 Slaterdeterminant set XML element.

<sposet_collection ...>
  <sposet name="spo" size="8">
    ...
  </sposet>
</sposet_collection>
<determinantset>
  <slaterdeterminant delay_rank="32">
    <determinant sposet="spo"/>
    <determinant sposet="spo"/>
  </slaterdeterminant>
</determinantset>

Additional information:

• delay_rank This option enables delayed updates of the Slater matrix inverse when particle-by-particle move is used. By default or if delay_rank=0 given in the input file, QMCPACK sets 1 for Slater matrices with a leading dimension \(<192\) and 32 otherwise. delay_rank=1 uses the Fahy’s variant [FWL90] of the Sherman-Morrison rank-1 update, which is mostly using memory bandwidth-bound BLAS-2 calls. With delay_rank>1, the delayed update algorithm [] turns most of the computation to compute bound BLAS-3 calls. Tuning this parameter is highly recommended to gain the best performance on medium-to-large problem sizes (\(>200\) electrons). We have seen up to an order of magnitude speedup on large problem sizes. When studying the performance of QMCPACK, a scan of this parameter is required and we recommend starting from 32. The best delay_rank giving the maximal speedup depends on the problem size. Usually the larger delay_rank corresponds to a larger problem size. On CPUs, delay_rank must be chosen as a multiple of SIMD vector length for good performance of BLAS libraries. The best delay_rank depends on the processor microarchitecture. GPU support is under development.

• gpu This option is only effective when GPU features are built. Default to using GPU. “omptarget”, “cuda”, “sycl”, “cpu” can be set to target a specific implementation, “yes”, “no” can be used to toggle on or off GPU acceleration.

• batch The default value is yes if gpu=yes and no otherwise.

• matrix_inverter. When the inversion happens on the GPU, additional GPU memory is needed. Support matrix:

Build condition \ matrix_inverter	host	gpu
CUDA/HIP/SYCL not enabled	running on host	running on host
CUDA/HIP/SYCL enabled and gpu==no	running on host	running on host
CUDA/HIP/SYCL enabled and gpu==yes	running on host	running on GPU

Multideterminant wavefunctions

multideterminant element:

Parent elements	determinantset
Child elements	detlist

Attribute:

Name	Datatype	Values	Default	Description
optimize	Text	yes/no	yes	Enable optimization.
spo_up	Text			The name of SPO for spin up electrons
spo_down	Text			The name of SPO for spin down electrons
algorithm	Text		precomputed_table_method	Slater matrix inversion scheme.

Table 3 Options for the multideterminant xml-block.

Additional information:

• algorithm algorithms used in multi-Slater determinant implementation. table_method table method of Clark et al. [] . precomputed_table_method adds partial sum precomputation on top of table_method.

• When the multideterminant wavefunction is read from an HDF5 file in the detlist child, the HDF5 dataset must use 64 bit unsigned integers to represent the determinants. The utils/determinants_tools.py script described in further detail below will check that the determinants are stored using the correct type and correct files that are storing signed 64 bit integers.

Listing 14 multideterminant set XML element.

<sposet_collection ...>
  <sposet name="spo" size="85">
    ...
  </sposet>
</sposet_collection>
<determinantset>
  <multideterminant optimize="yes" spo_up="spo" spo_dn="spo">
    <detlist size="1487" type="DETS" nca="0" ncb="0" nea="2" neb="2" nstates="85" cutoff="1e-20" href="LiH.orbs.h5">
  </multideterminant>
</determinantset>

Multiple schemes to generate a multideterminant wavefunction are possible, from CASSF to full CI or selected CI. The QMCPACK converter can convert MCSCF multideterminant wavefunctions from GAMESS [SBB+93] and CIPSI [EG13] wavefunctions from Quantum Package [Sce17] (QP). Full details of how to run a CIPSI calculation and convert the wavefunction for QMCPACK are given in CIPSI wavefunction interface.

The script utils/determinants_tools.py can be used to generate useful information about the multideterminant wavefunction. This script takes, as a required argument, the path of an h5 file corresponding to the wavefunction. Used without optional arguments, it prints the number of determinants, the number of CSFs, and a histogram of the excitation degree.

> determinants_tools.py ./tests/molecules/C2_pp/C2.h5
Summary:
excitation degree 0 count: 1
excitation degree 1 count: 6
excitation degree 2 count: 148
excitation degree 3 count: 27
excitation degree 4 count: 20

n_det 202
n_csf 104

If the --verbose argument is used, the script will print each determinant, the associated CSF, and the excitation degree relative to the first determinant.

> determinants_tools.py -v ./tests/molecules/C2_pp/C2.h5 | head
1
alpha  1111000000000000000000000000000000000000000000000000000000
beta   1111000000000000000000000000000000000000000000000000000000
scf    2222000000000000000000000000000000000000000000000000000000
excitation degree  0

2
alpha  1011100000000000000000000000000000000000000000000000000000
beta   1011100000000000000000000000000000000000000000000000000000
scf    2022200000000000000000000000000000000000000000000000000000
excitation degree  2

Orbital Rotation

Orbital rotation mixes orbitals between those occupied by electrons and those unoccupied by electrons. Because it changes the orbitals, a well-chosen optimized orbital rotation can improve the trial wavefunction for VMC, can change the nodal structure, and can potentially improve the fixed-node DMC energy.

Combining orbitals is complicated by the need to maintain the normalization of the orbitals. A rotation matrix will preserve the normalization of the vectors in linear combinations. However the entries in a rotation matrix are not independent. A rotation matrix can alternatively be expressed as the matrix exponential of a skew-symmetric matrix: \(R = \exp(\kappa)\). The entries in that skew-symmetric matrix are independent and can form an independent set of optimizable parameters.

Optimizable orbitals are given in the input file by enclosing an SPO in an rotated_sposet element. The determinant element id attribute should reference the name of the rotated sposet.

The rotated_sposet element requires use of the updated sposet_collection style.

rotated_sposet element:

Parent elements	sposet_collection
Child elements	sposet, opt_vars

Attribute:

Name	Datatype	Values	Default	Description
name	Text			Name of rotated SPOSet
method	Text	global/history	global	Rotation matrix composition method

Listing 15 Orbital Rotation XML element.

<sposet_collection ...>
  <rotated_sposet name="rot_spo">
    <sposet name="spo" size="8">
      ...
    </sposet>
  </rotated_sposet>
</sposet_collection>
<determinantset>
  <slaterdeterminant>
    <determinant sposet="rot_spo"/>
    <determinant sposet="rot_spo"/>
  </slaterdeterminant>
</determinantset>

The opt_vars element can be used to specify initial rotation parameters. The parameters are given as a space-separated list of numbers in the element text. The length of this list must match the expected number of rotation parameters.

Composing rotations

Rotation matrices do not commute, which consequently means the entries in the kappa matrix do not simply add when combining rotations. The parameters tracked for optimization are those for which the parameter derivatives are possibly non-zero. Rotations from one occupied orbital to another, or from on unoccupied orbital to another, have no effect on the energy, and hence have a zero parameter derivative. These parameters are a subset of the full number of parameters in the kappa matrix. When rotations are combined, the entries corresponding to zero parameter derivatives can take on a non-zero value (i.e. the kappa matrix gets ‘filled-in’).

There are two ways to handle this. One way is to store a list of applied rotations. This method applies a new rotation to the coefficient matrix, and updates the coefficient matrix at each optimization step. This is the “history” method.

\[C' = \exp(\kappa_n) \dots \exp(\kappa_1) \exp(\kappa_0) C\]

The other way is to track the full set of kappa values separately. After the matrix multiplication to compose the rotations, the matrix log recovers the new kappa matrix entries. This is the “global” method. This method keeps a separate copy of the coefficient matrix and updates it using the global rotation matrix at each optimization step.

\[\begin{split}\kappa_{new} &= \ln( \exp(\kappa_{\Delta}) \exp(\kappa_{old}) ) \\ C' &= \exp(\kappa_{new}) C\end{split}\]

Another consequence is the rotation parameters printed in the output are meaningless past the first rotation. Internally, the rotation code deals only with the difference between parameters at each step.

This also means that extra information needs to be stored with the results of the optimization. The extra information is stored in the VP HDF file.

Backflow Wavefunctions

One can perturb the nodal surface of a single-Slater/multi-Slater wavefunction through use of a backflow transformation. Specifically, if we have an antisymmetric function \(D(\mathbf{x}_{0\uparrow},\cdots,\mathbf{x}_{N\uparrow}, \mathbf{x}_{0\downarrow},\cdots,\mathbf{x}_{N\downarrow})\), and if \(i_\alpha\) is the \(i\)-th particle of species type \(\alpha\), then the backflow transformation works by making the coordinate transformation \(\mathbf{x}_{i_\alpha} \to \mathbf{x}'_{i_\alpha}\) and evaluating \(D\) at these new “quasiparticle” coordinates. QMCPACK currently supports quasiparticle transformations given by

(8)\[\mathbf{x}'_{i_\alpha}=\mathbf{x}_{i_\alpha}+\sum_{\alpha \leq \beta} \sum_{i_\alpha \neq j_\beta} \eta^{\alpha\beta}(|\mathbf{x}_{i_\alpha}-\mathbf{x}_{j_\beta}|)(\mathbf{x}_{i_\alpha}-\mathbf{x}_{j_\beta})\:.\]

Here, \(\eta^{\alpha\beta}(|\mathbf{x}_{i_\alpha}-\mathbf{x}_{j_\beta}|)\) is a radially symmetric backflow transformation between species \(\alpha\) and \(\beta\). In QMCPACK, particle \(i_\alpha\) is known as the “target” particle and \(j_\beta\) is known as the “source.” The main types of transformations are so-called one-body terms, which are between an electron and an ion \(\eta^{eI}(|\mathbf{x}_{i_e}-\mathbf{x}_{j_I}|)\) and two-body terms. Two-body terms are distinguished as those between like and opposite spin electrons: \(\eta^{e(\uparrow)e(\uparrow)}(|\mathbf{x}_{i_e(\uparrow)}-\mathbf{x}_{j_e(\uparrow)}|)\) and \(\eta^{e(\uparrow)e(\downarrow)}(|\mathbf{x}_{i_e(\uparrow)}-\mathbf{x}_{j_e(\downarrow)}|)\). Henceforth, we will assume that \(\eta^{e(\uparrow)e(\uparrow)}=\eta^{e(\downarrow)e(\downarrow)}\).

In the following, we explain how to describe general terms such as (8) in a QMCPACK XML file. For specificity, we will consider a particle set consisting of H and He (in that order). This ordering will be important when we build the XML file, so you can find this out either through your specific declaration of <particleset>, by looking at the hdf5 file in the case of plane waves, or by looking at the QMCPACK output file in the section labeled “Summary of QMC systems.”

Input specifications

All backflow declarations occur within a single <backflow> ... </backflow> block. Backflow transformations occur in <transformation> blocks and have the following input parameters:

Transformation element:

Name	Datatype	Values	Default	Description
name	Text		(Required)	Unique name for this Jastrow function.
type	Text	“e-I”	(Required)	Define a one-body backflow transformation.
	Text	“e-e”		Define a two-body backflow transformation.
function	Text	B-spline	(Required)	B-spline type transformation (no other types supported).
source	Text			“e” if two body, ion particle set if one body.

Just like one- and two-body jastrows, parameterization of the backflow transformations are specified within the <transformation> blocks by <correlation> blocks. Please refer to Spline form for more information.

Example Use Case

Having specified the general form, we present a general example of one-body and two-body backflow transformations in a hydrogen-helium mixture. The hydrogen and helium ions have independent backflow transformations, as do the like and unlike-spin two-body terms. One caveat is in order: ionic backflow transformations must be listed in the order they appear in the particle set. If in our example, helium is listed first and hydrogen is listed second, the following example would be correct. However, switching backflow declaration to hydrogen first then helium, will result in an error. Outside of this, declaration of one-body blocks and two-body blocks are not sensitive to ordering.

<backflow>
<!--The One-Body term with independent e-He and e-H terms. IN THAT ORDER -->
<transformation name="eIonB" type="e-I" function="Bspline" source="ion0">
    <correlation cusp="0.0" size="8" type="shortrange" init="no" elementType="He" rcut="3.0">
        <coefficients id="eHeC" type="Array" optimize="yes">
            0 0 0 0 0 0 0 0
        </coefficients>
    </correlation>
    <correlation cusp="0.0" size="8" type="shortrange" init="no" elementType="H" rcut="3.0">
        <coefficients id="eHC" type="Array" optimize="yes">
            0 0 0 0 0 0 0 0
        </coefficients>
    </correlation>
</transformation>

<!--The Two-Body Term with Like and Unlike Spins -->
<transformation name="eeB" type="e-e" function="Bspline" >
    <correlation cusp="0.0" size="7" type="shortrange" init="no" speciesA="u" speciesB="u" rcut="1.2">
        <coefficients id="uuB1" type="Array" optimize="yes">
            0 0 0 0 0 0 0
        </coefficients>
    </correlation>
    <correlation cusp="0.0" size="7" type="shortrange" init="no" speciesA="d" speciesB="u" rcut="1.2">
        <coefficients id="udB1" type="Array" optimize="yes">
            0 0 0 0 0 0 0
        </coefficients>
    </correlation>
</transformation>
</backflow>

Currently, backflow works only with single-Slater determinant wavefunctions. When a backflow transformation has been declared, it should be placed within the <determinantset> block, but outside of the <slaterdeterminant> blocks, like so:

<determinantset ... >
    <!--basis set declarations go here, if there are any -->

    <backflow>
        <transformation ...>
          <!--Here is where one and two-body terms are defined -->
         </transformation>
     </backflow>

     <slaterdeterminant>
         <!--Usual determinant definitions -->
     </slaterdeterminant>
 </determinantset>

Optimization Tips

Backflow is notoriously difficult to optimize—it is extremely nonlinear in the variational parameters and moves the nodal surface around. As such, it is likely that a full Jastrow+Backflow optimization with all parameters initialized to zero might not converge in a reasonable time. If you are experiencing this problem, the following pointers are suggested (in no particular order).

Get a good starting guess for \(\Psi_T\):

1. Try optimizing the Jastrow first without backflow.

2. Freeze the Jastrow parameters, introduce only the e-e terms in the backflow transformation, and optimize these parameters.

3. Freeze the e-e backflow parameters, and then optimize the e-I terms.

   • If difficulty is encountered here, try optimizing each species independently.

4. Unfreeze all Jastrow, e-e backflow, and e-I backflow parameters, and reoptimize.

Optimizing Backflow Terms

It is possible that the previous prescription might grind to a halt in steps 2 or 3 with the inability to optimize the e-e or e-I backflow transformation independently, especially if it is initialized to zero. One way to get around this is to build a good starting guess for the e-e or e-I backflow terms iteratively as follows:

1. Start off with a small number of knots initialized to zero. Set \(r_{cut}\) to be small (much smaller than an interatomic distance).

2. Optimize the backflow function.

3. If this works, slowly increase \(r_{cut}\) and/or the number of knots.

4. Repeat steps 2 and 3 until there is no noticeable change in energy or variance of \(\Psi_T\).

Tweaking the Optimization Run

The following modifications are worth a try in the optimization block:

• Try setting “useDrift” to “no.” This eliminates the use of wavefunction gradients and force biasing in the VMC algorithm. This could be an issue for poorly optimized wavefunctions with pathological gradients.

• Try increasing “exp0” in the optimization block. Larger values of exp0 cause the search directions to more closely follow those predicted by steepest-descent than those by the linear method.

Note that the new adaptive shift optimizer has not yet been tried with backflow wavefunctions. It should perform better than the older optimizers, but a considered optimization process is still recommended.

Jastrow Factors

Jastrow factors are among the simplest and most effective ways of including dynamical correlation in the trial many body wavefunction. The resulting many body wavefunction is expressed as the product of an antisymmetric (in the case of Fermions) or symmetric (for Bosons) part and a correlating Jastrow factor like so:

(9)\[\Psi(\vec{R}) = \mathcal{A}(\vec{R}) \exp\left[J(\vec{R})\right]\]

In this section we will detail the types and forms of Jastrow factor used in QMCPACK. Note that each type of Jastrow factor needs to be specified using its own individual jastrow XML element. For this reason, we have repeated the specification of the jastrow tag in each section, with specialization for the options available for that given type of Jastrow.

One-body Jastrow functions

The one-body Jastrow factor is a form that allows for the direct inclusion of correlations between particles that are included in the wavefunction with particles that are not explicitly part of it. The most common example of this are correlations between electrons and ions.

The Jastrow function is specified within a wavefunction element and must contain one or more correlation elements specifying additional parameters as well as the actual coefficients. Example use cases gives examples of the typical nesting of jastrow, correlation, and coefficient elements.

Input Specification

Jastrow element:

name	datatype	values	defaults	description
name	text		(required)	Unique name for this Jastrow function
type	text	One-body	(required)	Define a one-body function
function	text	Bspline	(required)	BSpline Jastrow
	text	pade2		Pade form
	text	…		…
source	text	name	(required)	Name of attribute of classical particle set
print	text	yes / no	yes	Jastrow factor printed in external file?

elements
	Correlation
Contents
	(None)

To be more concrete, the one-body Jastrow factors used to describe correlations between electrons and ions take the form below:

(10)\[J1=\sum_I^{ion0}\sum_i^e u_{ab}(|r_i-R_I|)\]

where I runs over all of the ions in the calculation, i runs over the electrons and \(u_{ab}\) describes the functional form of the correlation between them. Many different forms of \(u_{ab}\) are implemented in QMCPACK. We will detail two of the most common ones below.

Spline form

The one-body spline Jastrow function is the most commonly used one-body Jastrow for solids. This form was first described and used in [EKCS12]. Here \(u_{ab}\) is an interpolating 1D B-spline (tricublc spline on a linear grid) between zero distance and \(r_{cut}\). In 3D periodic systems the default cutoff distance is the Wigner Seitz cell radius. For other periodicities, including isolated molecules, the \(r_{cut}\) must be specified. The cusp can be set. \(r_i\) and \(R_I\) are most commonly the electron and ion positions, but any particlesets that can provide the needed centers can be used.

Correlation element:

Name	Datatype	Values	Defaults	Description
ElementType	Text	Name	See below	Classical particle target
SpeciesA	Text	Name	See below	Classical particle target
SpeciesB	Text	Name	See below	Quantum species target
Size	Integer	\(> 0\)	(Required)	Number of coefficients
Rcut	Real	\(> 0\)	See below	Distance at which the correlation goes to 0
Cusp	Real	\(\ge 0\)	0	Value for use in Kato cusp condition
Spin	Text	Yes or no	No	Spin dependent Jastrow factor

Elements
	Coefficients
Contents
	(None)

Additional information:

• elementType, speciesA, speciesB, spin

  For a spin-independent Jastrow factor (spin = “no”), elementType should be the name of the group of ions in the classical particleset to which the quantum particles should be correlated. For a spin-dependent Jastrow factor (spin = “yes”), set speciesA to the group name in the classical particleset and speciesB to the group name in the quantum particleset.

• rcut

  The cutoff distance for the function in atomic units (bohr). For 3D fully periodic systems, this parameter is optional, and a default of the Wigner Seitz cell radius is used. Otherwise this parameter is required.

• cusp

  The one-body Jastrow factor can be used to make the wavefunction satisfy the electron-ion cusp condition :cite:kato. In this case, the derivative of the Jastrow factor as the electron approaches the nucleus will be given by

(11)\[\left(\frac{\partial J}{\partial r_{iI}}\right)_{r_{iI} = 0} = -Z .\]

Note that if the antisymmetric part of the wavefunction satisfies the electron-ion cusp condition (for instance by using single-particle orbitals that respect the cusp condition) or if a nondivergent pseudopotential is used, the Jastrow should be cuspless at the nucleus and this value should be kept at its default of 0.

Coefficients element:

Name	Datatype	Values	Defaults	Description
Id	Text		(Required)	Unique identifier
Type	Text	Array	(Required)
Optimize	Text	Yes or no	Yes	if no, values are fixed in optimizations
Elements
(None)
Contents
(No name)	Real array		Zeros	Jastrow coefficients

Example use cases

Specify a spin-independent function with four parameters. Because rcut is not specified, the default cutoff of the Wigner Seitz cell radius is used; this Jastrow must be used with a 3D periodic system such as a bulk solid. The name of the particleset holding the ionic positions is “i.”

<jastrow name="J1" type="One-Body" function="Bspline" print="yes" source="i">
 <correlation elementType="C" cusp="0.0" size="4">
   <coefficients id="C" type="Array"> 0  0  0  0  </coefficients>
 </correlation>
</jastrow>

Specify a spin-dependent function with seven up-spin and seven down-spin parameters. The cutoff distance is set to 6 atomic units. Note here that the particleset holding the ions is labeled as ion0 rather than “i,” as in the other example. Also in this case, the ion is lithium with a coulomb potential, so the cusp condition is satisfied by setting cusp=”d.”

<jastrow name="J1" type="One-Body" function="Bspline" source="ion0" spin="yes">
  <correlation speciesA="Li" speciesB="u" size="7" rcut="6">
    <coefficients id="eLiu" cusp="3.0" type="Array">
    0.0 0.0 0.0 0.0 0.0 0.0 0.0
    </coefficients>
  </correlation>
  <correlation speciesA="C" speciesB="d" size="7" rcut="6">
    <coefficients id="eLid" cusp="3.0" type="Array">
    0.0 0.0 0.0 0.0 0.0 0.0 0.0
    </coefficients>
  </correlation>
</jastrow>

Pade form

Although the spline Jastrow factor is the most flexible and most commonly used form implemented in QMCPACK, there are times where its flexibility can make it difficult to optimize. As an example, a spline Jastrow with a very large cutoff can be difficult to optimize for isolated systems such as molecules because of the small number of samples present in the tail of the function. In such cases, a simpler functional form might be advantageous. The second-order Pade Jastrow factor, given in (12), is a good choice in such cases.

(12)\[u_{ab}(r) = \frac{a*r+c*r^2}{1+b*r}\]

Unlike the spline Jastrow factor, which includes a cutoff, this form has an infinite range and will be applied to every particle pair (subject to the minimum image convention). It also is a cuspless Jastrow factor, so it should be used either in combination with a single particle basis set that contains the proper cusp or with a smooth pseudopotential.

Correlation element:

Name	Datatype	Values	Defaults	Description
ElementType	Text	Name	See below	Classical particle target
Elements
	Coefficients
Contents
	(None)

Parameter element:

Name	Datatype	Values	Defaults	Description
Id	String	Name	(Required)	Name for variable
Name	String	A or B or C	(Required)	See (12)
Optimize	Text	Yes or no	Yes	If no, values are fixed in optimizations

Elements
(None)
Contents
(No name)	Real	Parameter value	(Required)	Jastrow coefficients

Example use case

Specify a spin-independent function with independent Jastrow factors for two different species (Li and H). The name of the particleset holding the ionic positions is “i.”

<jastrow name="J1" function="pade2" type="One-Body" print="yes" source="i">
  <correlation elementType="Li">
    <var id="LiA" name="A">  0.34 </var>
    <var id="LiB" name="B"> 12.78 </var>
    <var id="LiC" name="C">  1.62 </var>
  </correlation>
  <correlation elementType="H"">
    <var id="HA" name="A">  0.14 </var>
    <var id="HB" name="B"> 6.88 </var>
    <var id="HC" name="C"> 0.237 </var>
  </correlation>
</jastrow>

Short Range Cusp Form

The idea behind this functor is to encode nuclear cusps and other details at very short range around a nucleus in the region that the Gaussian orbitals of quantum chemistry are not capable of describing correctly. The functor is kept short ranged, because outside this small region, quantum chemistry orbital expansions are already capable of taking on the correct shapes. Unlike a pre-computed cusp correction, this optimizable functor can respond to changes in the wave function during VMC optimization. The functor’s form is

(13)\[u(r) = -\exp{\left(-r/R_0\right)} \left( A R_0 + \sum_{k=0}^{N-1} B_k \frac{ (r/R_0)^{k+2} }{ 1 + (r/R_0)^{k+2} } \right)\]

in which \(R_0\) acts as a soft cutoff radius (\(u(r)\) decays to zero quickly beyond roughly this distance) and \(A\) determines the cusp condition.

(14)\[\lim_{r \to 0} \frac{\partial u}{\partial r} = A\]

The simple exponential decay is modified by the \(N\) coefficients \(B_k\) that define an expansion in sigmoidal functions, thus adding detailed structure in a short-ranged region around a nucleus while maintaining the correct cusp condition at the nucleus. Note that sigmoidal functions are used instead of, say, a bare polynomial expansion, as they trend to unity past the soft cutoff radius and so interfere less with the exponential decay that keeps the functor short ranged. Although \(A\), \(R_0\), and the \(B_k\) coefficients can all be optimized as variational parameters, \(A\) will typically be fixed as the desired cusp condition is known.

To specify this one-body Jastrow factor, use an input section like the following.

<jastrow name="J1Cusps" type="One-Body" function="shortrangecusp" source="ion0" print="yes">
  <correlation rcut="6" cusp="3" elementType="Li">
    <var id="LiCuspR0" name="R0" optimize="yes"> 0.06 </var>
    <coefficients id="LiCuspB" type="Array" optimize="yes">
      0 0 0 0 0 0 0 0 0 0
    </coefficients>
  </correlation>
  <correlation rcut="6" cusp="1" elementType="H">
    <var id="HCuspR0" name="R0" optimize="yes"> 0.2 </var>
    <coefficients id="HCuspB" type="Array" optimize="yes">
      0 0 0 0 0 0 0 0 0 0
    </coefficients>
  </correlation>
</jastrow>

Here “rcut” is specified as the range beyond which the functor is assumed to be zero. The value of \(A\) can either be specified via the “cusp” option as shown above, in which case its optimization is disabled, or through its own “var” line as for \(R_0\), in which case it can be specified as either optimizable (“yes”) or not (“no”). The coefficients \(B_k\) are specified via the “coefficients” section, with the length \(N\) of the expansion determined automatically based on the length of the array.

Note that this one-body Jastrow form can (and probably should) be used in conjunction with a longer ranged one-body Jastrow, such as a spline form. Be sure to set the longer-ranged Jastrow to be cusp-free!

Two-body Jastrow functions

The two-body Jastrow factor is a form that allows for the explicit inclusion of dynamic correlation between two particles included in the wavefunction. It is almost always given in a spin dependent form so as to satisfy the Kato cusp condition between electrons of different spins [].

The two body Jastrow function is specified within a wavefunction element and must contain one or more correlation elements specifying additional parameters as well as the actual coefficients. Example use cases gives examples of the typical nesting of jastrow, correlation and coefficient elements.

Input Specification

Jastrow element:

name	datatype	values	defaults	description
name	text		(required)	Unique name for this Jastrow function
type	text	Two-body	(required)	Define a one-body function
function	text	Bspline	(required)	BSpline Jastrow
print	text	yes / no	yes	Jastrow factor printed in external file?
elements
	Correlation
Contents
	(None)

The two-body Jastrow factors used to describe correlations between electrons take the form

(15)\[J2=\sum_i^{e}\sum_{j>i}^{e} u_{ab}(|r_i-r_j|)\]

The most commonly used form of two body Jastrow factor supported by the code is a splined Jastrow factor, with many similarities to the one body spline Jastrow.

Spline form

The two-body spline Jastrow function is the most commonly used two-body Jastrow for solids. This form was first described and used in [EKCS12]. Here \(u_{ab}\) is an interpolating 1D B-spline (tricublc spline on a linear grid) between zero distance and \(r_{cut}\). In 3D periodic systems, the default cutoff distance is the Wigner Seitz cell radius. For other periodicities, including isolated molecules, the \(r_{cut}\) must be specified. \(r_i\) and \(r_j\) are typically electron positions. The cusp condition as \(r_i\) approaches \(r_j\) is set by the relative spin of the electrons.

Correlation element:

Name	Datatype	Values	Defaults	Description
SpeciesA	Text	U or d	(Required)	Quantum species target
SpeciesB	Text	U or d	(Required)	Quantum species target
Size	Integer	\(> 0\)	(Required)	Number of coefficients
Rcut	Real	\(> 0\)	See below	Distance at which the correlation goes to 0
Spin	Text	Yes or no	No	Spin-dependent Jastrow factor
Elements
	Coefficients
Contents
	(None)

Additional information:

• speciesA, speciesB The scale function u(r) is defined for species pairs uu and ud. There is no need to define ud or dd since uu=dd and ud=du. The cusp condition is computed internally based on the charge of the quantum particles.

Coefficients element:

Name	Datatype	Values	Defaults	Description
Id	Text		(Required)	Unique identifier
Type	Text	Array	(Required)
Optimize	Text	Yes or no	Yes	If no, values are fixed in optimizations
Elements
(None)
Contents
(No name)	Real array		Zeros	Jastrow coefficients

Example use cases

Specify a spin-dependent function with four parameters for each channel. In this case, the cusp is set at a radius of 4.0 bohr (rather than to the default of the Wigner Seitz cell radius). Also, in this example, the coefficients are set to not be optimized during an optimization step.

<jastrow name="J2" type="Two-Body" function="Bspline" print="yes">
  <correlation speciesA="u" speciesB="u" size="8" rcut="4.0">
    <coefficients id="uu" type="Array" optimize="no"> 0.2309049836 0.1312646071 0.05464141356 0.01306231516</coefficients>
  </correlation>
  <correlation speciesA="u" speciesB="d" size="8" rcut="4.0">
    <coefficients id="ud" type="Array" optimize="no"> 0.4351561096 0.2377951747 0.1129144262 0.0356789236</coefficients>
  </correlation>
</jastrow>

User defined functional form

To aid in implementing different forms for \(u_{ab}(r)\), there is a script that uses a symbolic expression to generate the appropriate code (with spatial and parameter derivatives). The script is located in src/QMCWaveFunctions/Jastrow/codegen/user_jastrow.py. The script requires Sympy (www.sympy.org) for symbolic mathematics and code generation.

To use the script, modify it to specify the functional form and a list of variational parameters. Optionally, there may be fixed parameters - ones that are specified in the input file, but are not part of the variational optimization. Also one symbol may be specified that accepts a cusp value in order to satisfy the cusp condition. There are several example forms in the script. The default form is the simple Padé.

Once the functional form and parameters are specified in the script, run the script from the codegen directory and recompile QMCPACK. The main output of the script is the file src/QMCWaveFunctions/Jastrow/UserFunctor.h. The script also prints information to the screen, and one section is a sample XML input block containing all the parameters.

There is a unit test in src/QMCWaveFunctions/test/test_user_jastrow.cpp to perform some minimal testing of the Jastrow factor. The unit test will need updating to properly test new functional forms. Most of the changes relate to the number and name of variational parameters.

Jastrow element:

name	datatype	values	defaults	description
name	text		(required)	Unique name for this Jastrow function
type	text	One-body	(required)	Define a one-body function
		Two-body	(required)	Define a two-body function
function	text	user	(required)	User-defined functor

See other parameters as appropriate for one or two-body functions

elements
	Correlation
Contents
	(None)

Long-ranged Jastrow factors

While short-ranged Jastrow factors capture the majority of the benefit for minimizing the total energy and the energy variance, long-ranged Jastrow factors are important to accurately reproduce the short-ranged (long wavelength) behavior of quantities such as the static structure factor, and are therefore essential for modern accurate finite size corrections in periodic systems.

Below two types of long-ranged Jastrow factors are described. The first (the k-space Jastrow) is simply an expansion of the one and/or two body correlation functions in plane waves, with the coefficients comprising the optimizable parameters. The second type have few variational parameters and use the optimized breakup method of Natoli and Ceperley [NC95] (the Yukawa and Gaskell RPA Jastrows).

Long-ranged Jastrow: k-space Jastrow

The k-space Jastrow introduces explicit long-ranged dependence commensurate with the periodic supercell. This Jastrow is to be used in periodic boundary conditions only.

The input for the k-space Jastrow fuses both one and two-body forms into a single element and so they are discussed together here. The one- and two-body terms in the k-Space Jastrow have the form:

(16)\[J_1 = \sum_{G\ne 0}b_G\rho_G^I\rho_{-G}\]

(17)\[J_2 = \sum_{G\ne 0}a_G\rho_G\rho_{-G}\]

Here \(\rho_G\) is the Fourier transform of the instantaneous electron density:

(18)\[\rho_G=\sum_{n\in electrons}e^{iG\cdot r_n}\]

and \(\rho_G^I\) has the same form, but for the fixed ions. In both cases the coefficients are restricted to be real, though in general the coefficients for the one-body term need not be. See Feature: Reciprocal-space Jastrow factors for more detail.

Input for the k-space Jastrow follows the familar nesting of jastrow-correlation-coefficients elements, with attributes unique to the k-space Jastrow at the correlation input level.

jastrow type=kSpace element:

parent elements:	wavefunction
child elements:	correlation

attributes:

Name	Datatype	Values	Default	Description
type\(^r\)	text	kSpace		must be kSpace
name\(^r\)	text	anything	0	Unique name for Jastrow
source\(^r\)	text	particleset.name		Ion particleset name

correlation element:

parent elements:	jastrow type=kSpace
child elements:	coefficients

attributes:

Name	Datatype	Values	Default	Description
type\(^r\)	text	One-body, Two-Body		Must be One-body/Two-body
kc\(^r\)	real	kc \(\ge\) 0	0.0	k-space cutoff in a.u.
symmetry\(^o\)	text	crystal,isotropic,none	crystal	symmetry of coefficients
spinDependent\(^o\)	boolean	yes,no	no	No current function

coefficients element:

parent elements:	correlation
child elements:	None

attributes:

Name	Datatype	Values	Default	Description
id\(^r\)	text	anything	cG1/cG2	Label for coeffs
type\(^r\)	text	Array	0	Must be Array

body text: The body text is a list of real values for the parameters.

Additional information:

• It is normal to provide no coefficients as an initial guess. The number of coefficients will be automatically calculated according to the k-space cutoff + symmetry and set to zero.

• Providing an incorrect number of parameters also results in all parameters being set to zero.

• There is currently no way to turn optimization on/off for the k-space Jastrow. The coefficients are always optimized.

• Spin dependence is currently not implemented for this Jastrow.

• kc: Parameters with G vectors magnitudes less than kc are included in the Jastrow. If kc is zero, it is the same as excluding the k-space term.

• symmetry=crystal: Impose crystal symmetry on coefficients according to the structure factor.

• symmetry=isotropic: Impose spherical symmetry on coefficients according to G-vector magnitude.

• symmetry=none: Impose no symmetry on the coefficients.

Listing 16 k-space Jastrow with one- and two-body terms.

<jastrow type="kSpace" name="Jk" source="ion0">
  <correlation kc="4.0" type="One-Body" symmetry="cystal">
    <coefficients id="cG1" type="Array">
    </coefficients>
  </correlation>
  <correlation kc="4.0" type="Two-Body" symmetry="crystal">
    <coefficients id="cG2" type="Array">
    </coefficients>
 </correlation>
</jastrow>

Listing 17 k-space Jastrow with one-body term only.

<jastrow type="kSpace" name="Jk" source="ion0">
   <correlation kc="4.0" type="One-Body" symmetry="crystal">
      <coefficients id="cG1" type="Array">
      </coefficients>
   </correlation>
</jastrow>

Listing 18 k-space Jastrow with two-body term only.

<jastrow type="kSpace" name="Jk" source="ion0">
   <correlation kc="4.0" type="Two-Body" symmetry="crystal">
      <coefficients id="cG2" type="Array">
      </coefficients>
   </correlation>
</jastrow>

Long-ranged Jastrows: Gaskell RPA and Yukawa forms

NOTE: The Yukawa and RPA Jastrows do not work at present and are currently being revived. Please contact the developers if you are interested in using them.

The exact Jastrow correlation functions contain terms which have a form similar to the Coulomb pair potential. In periodic systems the Coulomb potential is replaced by an Ewald summation of the bare potential over all periodic image cells. This sum is often handled by the optimized breakup method [NC95] and this same approach is applied to the long-ranged Jastrow factors in QMCPACK.

There are two main long-ranged Jastrow factors of this type implemented in QMCPACK: the Gaskell RPA [] form and the [] form. Both of these forms were used by Ceperley in early studies of the electron gas [], but they are also appropriate starting points for general solids.

The Yukawa form is defined in real space. It’s long-range form is formally defined as

(19)\[u_Y^{PBC}(r) = \sum_{L\ne 0}\sum_{i<j}u_Y(\left|{r_i-r_j+L}\right|)\]

with \(u_Y(r)\) given by

(20)\[u_Y(r) = \frac{a}{r}\left(1-e^{-r/b}\right)\]

In QMCPACK a slightly more restricted form is used:

(21)\[u_Y(r) = \frac{r_s}{r}\left(1-e^{-r/\sqrt{r_s}}\right)\]

here “\(r_s\)” is understood to be a variational parameter.

The Gaskell RPA form—which contains correct short/long range limits and minimizes the total energy of the electron gas within the RPA—is defined directly in k-space:

(22)\[u_{RPA}(k) = -\frac{1}{2S_0(k)}+\frac{1}{2}\left(\frac{1}{S_0(k)^2}+\frac{4m_ev_k}{\hbar^2k^2}\right)^{1/2}\]

where $v_k$ is the Fourier transform of the Coulomb potential and \(S_0(k)\) is the static structure factor of the non-interacting electron gas:

\[\begin{split}S_0(k) = \left. \begin{cases} 1 & k>2k_F \\ \frac{3k}{4k_F}-\frac{1}{2}\left(\frac{k}{2k_F}\right)^3 & k<2k_F \end{cases} \right.\end{split}\]

When written in atomic units, RPA Jastrow implemented in QMCPACK has the form

(23)\[u_{RPA}(k) = \frac{1}{2N_e}\left(-\frac{1}{S_0(k)}+\left(\frac{1}{S_0(k)^2}+\frac{12}{r_s^3k^4}\right)^{1/2}\right)\]

Here “\(r_s\)” is again a variational parameter and \(k_F\equiv(\tfrac{9\pi}{4r_s^3})^{1/3}\).

For both the Yukawa and Gaskell RPA Jastrows, the default value for \(r_s\) is \(r_s=(\tfrac{3\Omega}{4\pi N_e})^{1/3}\).

jastrow type=Two-Body function=rpa/yukawa element:

parent elements:	wavefunction
child elements:	correlation

attributes:

Name	Datatype	Values	Default	Description
type\(^r\)	text	Two-body		Must be two-body
function\(^r\)	text	rpa/yukawa		Must be rpa or yukawa
name\(^r\)	text	anything	RPA_Jee	Unique name for Jastrow
longrange\(^o\)	boolean	yes/no	yes	Use long-range part
shortrange\(^o\)	boolean	yes/no	yes	Use short-range part

parameters:

Name	Datatype	Values	Default	Description
rs\(^o\)	rs	\(r_s>0\)	\(\tfrac{3\Omega}{4\pi N_e}\)	Avg. elec-elec distance
kc\(^o\)	kc	\(k_c>0\)	\(2\left(\tfrac{9\pi}{4}\right)^{1/3}\tfrac{4\pi N_e}{3\Omega}\)	k-space cutoff

Listing 19 Two body RPA Jastrow with long- and short-ranged parts.

<jastrow name=''Jee'' type=''Two-Body'' function=''rpa''>
</jastrow>

Three-body Jastrow functions

Explicit three-body correlations can be included in the wavefunction via the three-body Jastrow factor. The three-body electron-electron-ion correlation function (\(u_{\sigma\sigma'I}\)) currently used in is identical to the one proposed in []:

(24)\[\begin{split} \begin{aligned} u_{\sigma\sigma'I}(r_{\sigma I},r_{\sigma'I},r_{\sigma\sigma'}) &= \sum_{\ell=0}^{M_{eI}}\sum_{m=0}^{M_{eI}}\sum_{n=0}^{M_{ee}}\gamma_{\ell mn} r_{\sigma I}^\ell r_{\sigma'I}^m r_{\sigma\sigma'}^n \\ &\times \left(r_{\sigma I}-\frac{r_c}{2}\right)^3 \Theta\left(r_{\sigma I}-\frac{r_c}{2}\right) \nonumber \\ &\times \left(r_{\sigma' I}-\frac{r_c}{2}\right)^3 \Theta\left(r_{\sigma' I}-\frac{r_c}{2}\right) \nonumber\end{aligned}\end{split}\]

Here \(M_{eI}\) and \(M_{ee}\) are the maximum polynomial orders of the electron-ion and electron-electron distances, respectively, \(\{\gamma_{\ell mn}\}\) are the optimizable parameters (modulo constraints), \(r_c\) is a cutoff radius, and \(r_{ab}\) are the distances between electrons or ions \(a\) and \(b\). i.e. The correlation function is only a function of the interparticle distances and not a more complex function of the particle positions, \(\mathbf{r}\). As indicated by the \(\Theta\) functions, correlations are set to zero beyond a distance of \(r_c/2\) in either of the electron-ion distances and the largest meaningful electron-electron distance is \(r_c\). This is the highest-order Jastrow correlation function currently implemented.

Today, solid state applications of QMCPACK usually utilize one and two-body B-spline Jastrow functions, with calculations on heavier elements often also using the three-body term described above.

Example use case

Here is an example of H2O molecule. After optimizing one and two body Jastrow factors, add the following block in the wavefunction. The coefficients will be filled zero automatically if not given.

<jastrow name="J3" type="eeI" function="polynomial" source="ion0" print="yes">
  <correlation ispecies="O" especies="u" isize="3" esize="3" rcut="10">
    <coefficients id="uuO" type="Array" optimize="yes"> </coefficients>
  </correlation>
  <correlation ispecies="O" especies1="u" especies2="d" isize="3" esize="3" rcut="10">
    <coefficients id="udO" type="Array" optimize="yes"> </coefficients>
  </correlation>
  <correlation ispecies="H" especies="u" isize="3" esize="3" rcut="10">
    <coefficients id="uuH" type="Array" optimize="yes"> </coefficients>
  </correlation>
  <correlation ispecies="H" especies1="u" especies2="d" isize="3" esize="3" rcut="10">
    <coefficients id="udH" type="Array" optimize="yes"> </coefficients>
  </correlation>
</jastrow>

Gaussian Product Wavefunction

The Gaussian Product wavefunction implements (25)

(25)\[\Psi(\vec{R}) = \prod_{i=1}^N \exp\left[ -\frac{(\vec{R}_i-\vec{R}_i^o)^2}{2\sigma_i^2} \right]\]

where \(\vec{R}_i\) is the position of the \(i^{\text{th}}\) quantum particle and \(\vec{R}_i^o\) is its center. \(\sigma_i\) is the width of the Gaussian orbital around center \(i\).

This variational wavefunction enhances single-particle density at chosen spatial locations with adjustable strengths. It is useful whenever such localization is physically relevant yet not captured by other parts of the trial wavefunction. For example, in an electron-ion simulation of a solid, the ions are localized around their crystal lattice sites. This single-particle localization is not captured by the ion-ion Jastrow. Therefore, the addition of this localization term will improve the wavefunction. The simplest use case of this wavefunction is perhaps the quantum harmonic oscillator (please see the “tests/models/sho” folder for examples).

Input specification

Gaussian Product Wavefunction (ionwf):

Name	Datatype	Values	Default	Description
Name	Text	ionwf	(Required)	Unique name for this wavefunction
Width	Floats	1.0 -1	(Required)	Widths of Gaussian orbitals
Source	Text	ion0	(Required)	Name of classical particle set

Additional information:

• width There must be one width provided for each quantum particle. If a negative width is given, then its corresponding Gaussian orbital is removed. Negative width is useful if one wants to use Gaussian wavefunction for a subset of the quantum particles.

• source The Gaussian centers must be specified in the form of a classical particle set. This classical particle set is likely the ion positions “ion0,” hence the name “ionwf.” However, arbitrary centers can be defined using a different particle set. Please refer to the examples in “tests/models/sho.”

Example Use Case

<qmcsystem>
  <simulationcell>
    <parameter name="bconds">
          n n n
    </parameter>
  </simulationcell>
  <particleset name="e">
    <group name="u" size="1">
      <parameter name="mass">5.0</parameter>
      <attrib name="position" datatype="posArray" condition="0">
        0.0001 -0.0001 0.0002
      </attrib>
    </group>
  </particleset>
  <particleset name="ion0" size="1">
    <group name="H">
      <attrib name="position" datatype="posArray" condition="0">
        0 0 0
      </attrib>
    </group>
  </particleset>
  <wavefunction target="e" id="psi0">
    <ionwf name="iwf" source="ion0" width="0.8165"/>
  </wavefunction>
  <hamiltonian name="h0" type="generic" target="e">
    <extpot type="HarmonicExt" mass="5.0" energy="0.3"/>
    <estimator type="latticedeviation" name="latdev"
      target="e"    tgroup="u"
      source="ion0" sgroup="H"/>
  </hamiltonian>
</qmcsystem>

AlfeG04

D. Alfè and M. J. Gillan. An efficient localized basis set for quantum Monte Carlo calculations on condensed matter. Physical Review B, 70(16):161101, 2004.

FWL90

S. Fahy, X. W. Wang, and Steven G. Louie. Variational quantum Monte Carlo nonlocal pseudopotential approach to solids: Formulation and application to diamond, graphite, and silicon. Physical Review B, 42(6):3503–3522, 1990. doi:10.1103/PhysRevB.42.3503.

LEKS18

Ye Luo, Kenneth P. Esler, Paul R. C. Kent, and Luke Shulenburger. An efficient hybrid orbital representation for quantum monte carlo calculations. The Journal of Chemical Physics, 149(8):084107, 2018.